由于联考考到了树上莫队，然后我预处理和正解一样，就是单纯打不出来树上莫队，于是来写一发学习笔记。

'树’上莫队

应该没有人直接写在树上莫队的吧，都是把树转化成欧拉序的吧。

欧拉序好像就是括号序，但是记录的是节点编号，不是点权或者点上颜色。（考试时的误区，导致没有手胡出来代码）

然后再通过节点编号定位获取相应信息。

如果节点编号出现两次，那么就无视这个点。

欧拉序举例：

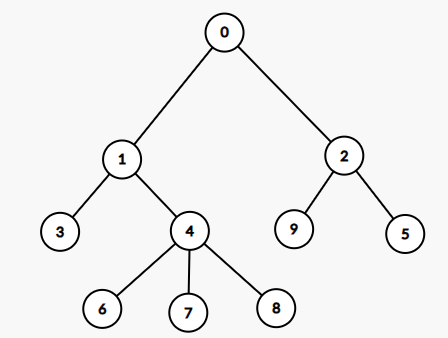
这个树按重链剖分来说的欧拉序是 [0,1,4,6,6,7,7,8,8,4,3,3,1,2,9,9,5,5,2,0][0,1,4,6,6,7,7,8,8,4,3,3,1,2,9,9,5,5,2,0]。

我们可以从中发现一些规律。

令 st[a]st[a] 为编号 aa 第一次出现的位置，ed[a]ed[a] 为编号 aa 第二次出现的位置。

如果此时我们要询问路径 7→27\to 2，发现 dfn7<dfn2dfn_7<dfn_2，那么取 [ed[7],st[2]][ed[7],st[2]] 作为询问的区间。按刚刚的策略 如果节点编号出现两次，那么就无视这个点 可以发现，这个区间可以转化：

{7,8,8,4,3,3,1,2}⇒{7,4,1,2}\{7,8,8,4,3,3,1,2\}\Rightarrow\{7,4,1,2\}

再举个栗子：路径 3→43\to 4 怎么转化？

发现 dfn4<dfn3dfn_4<dfn_3，则取 [ed[4],st[3]][ed[4],st[3]] 区间进行询问，转化为 {4,3}\{4,3\}。

发现这两个例子的 LCALCA 都正好没有统计到，所以要加上起点和终点的 LCALCA 的贡献。

但是如果 uu 是 vv 的祖先时，就不能再加一遍 LCALCA 了。

例题

板子题：SP10707

很惨的是，如果联考的时候这道题会，那么就是标准 std 了。/dk

因为权值很大，所以要离散化。

喜报，作者因为用了 unordered_map 然后卡常卡了 1h1h，然后换成离散化就过了。unordered_map 狗都不用，草！

注意细节即可。代码里有注释。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#include<bits/stdc++.h>
using namespace std;
struct line{
	int to,link;
}E[800002];
int head[500001],tot=1;
void addE(int u,int v){
	E[++tot].to=v;
	E[tot].link=head[u];
	head[u]=tot;
	return;
}
int dep[500001],siz[500001],fa[500001],hson[500001];
void dfs1(int now,int f){
	fa[now]=f;
	siz[now]=1;
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==f)continue;
		dep[E[i].to]=dep[now]+1;
		dfs1(E[i].to,now);
		siz[now]+=siz[E[i].to];
		if(siz[E[i].to]>siz[hson[now]])hson[now]=E[i].to;
	}
	return;
}
int dfn[400001],_dfn[400001],rk[800001],dfncnt,ltop[50001];
void dfs2(int now,int top){
	ltop[now]=top;
	dfn[now]=++dfncnt;
	rk[dfncnt]=now;
	if(!hson[now]){
		_dfn[now]=++dfncnt;//!!!!别忘了这里return的时候也要加_dfn数组
		rk[dfncnt]=now;
		return;
	}
	dfs2(hson[now],top);
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==fa[now]||E[i].to==hson[now])continue;
		dfs2(E[i].to,E[i].to);
	}
	_dfn[now]=++dfncnt;
	rk[dfncnt]=now;
	return;
}
int w[400001];
int LCA(int u,int v){
	while(ltop[u]!=ltop[v]){
		if(dep[ltop[u]]>dep[ltop[v]])u=fa[ltop[u]];
		else v=fa[ltop[v]];
	}
	return ((dep[u]>dep[v])?v:u);
}
int mp[500001];
int cnt=0,base,tes[500001];
struct query{
	int u,v,lca;
	int l,r,id;
	void init(){
		lca=LCA(u,v);
		if(dfn[u]>dfn[v])swap(u,v);
		if(u==lca)l=dfn[u],r=dfn[v],lca=0;
		else l=_dfn[u],r=dfn[v];
		return;
	}
	bool operator < (const query &a) const {
		return (l/base==a.l/base)?r<a.r:l<a.l;
	}
}Q[400004];
int bu[400001],Ans[400001];
inline void upd(const int t){
	bu[rk[t]]^=1;
	if(bu[rk[t]]){
		mp[w[rk[t]]]=mp[w[rk[t]]]+1;
		if(mp[w[rk[t]]]==1)cnt++;
	}
	else{
		if(mp[w[rk[t]]]==1)cnt--;
		mp[w[rk[t]]]=mp[w[rk[t]]]-1;
	}
	return;
}
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>w[i],tes[i]=w[i];
	sort(tes+1,tes+n+1);
	for(int i=1;i<=n;i++)w[i]=lower_bound(tes+1,tes+n+1,w[i])-tes;
	int x,y;
	for(int i=1;i<n;i++){
		cin>>x>>y;
		addE(x,y);
		addE(y,x);
	}
	dfs1(1,0);
	dfs2(1,1);
	for(int i=1;i<=m;i++){
		cin>>Q[i].u>>Q[i].v;
		Q[i].init();
		Q[i].id=i;
	}
	base=n*2/sqrt(m*2/3);
	sort(Q+1,Q+m+1);
	int l=1,r=0;
	for(int i=1;i<=m;i++){
		while(l>Q[i].l)upd(--l);
		while(l<Q[i].l)upd(l++);
		while(r>Q[i].r)upd(r--);
		while(r<Q[i].r)upd(++r);
//		cerr<<cnt<<"\n";
		if(Q[i].lca)upd(dfn[Q[i].lca]);//注意这里是dfn序
		Ans[Q[i].id]=cnt;
//		cerr<<cnt<<" "<<Q[i].len<<" "<<Q[i].lca<<"\n";
		if(Q[i].lca)upd(dfn[Q[i].lca]);
	}
	for(int i=1;i<=m;i++){
		cout<<Ans[i]<<"\n";
	}
	return 0;
}

20231012T3

考虑转换问题即可。

预处理质数的平方，暴力将原来的权值中间的平方因子除掉，然后就变成了是否有一种一个点对的权值相同。

考虑存在时，直接判断路径上的点数是否和颜色数是否相等即可。

代码就不贴了。

有其他例题欢迎在评论区提出。