字符串哈希

定义一个字符串到整数的映射 $f$ ，称为 Hash 函数。Hash 的核心思想是将输入的字符串转化为整数方便比较。

哈希方式

通用的方法是把字符串看成一个 $base$ 进制的数，即 $f_i=f_{i-1}\times base+s_i$ 。

这种哈希方法需要对大质数取模或者使用自然溢出。

不难发现这种方法存在类通项公式：

f_i=s_1\times base^{i-1}+s_2\times base^{i-2}+\cdots+s_i\times base^0

不难发现区间 $[l,r]$ 所形成的子串的哈希值是 $f_r-f_{l-1}\times base^{r-l+1}$ 。预处理 $base$ 的幂可以做到 $O(1)$ 处理子串哈希值。

哈希错误率

取模数为 $10^9+7$ ，经过计算可得正确率：

$O(n)=10^4$ ，有 $P=95.12\%$ 。
$O(n)=10^5$ ，有 $P<0.1\%$ 。

发现在大数据情况下极其容易出现哈希碰撞。

所以，对于较大的数据，可以对两个不同的大质数取模，或者取多个不同的 $base$ ，称作 多哈希。

哈希经典应用

字符串匹配

取模式串的哈希值，预处理文本串哈希值， $O(1)$ 求出文本串中每个与模式串长度相同的子串的哈希值进行比较即可。

最长回文子串

可以枚举回文中心（有 $2n$ 个）然后二分答案，时间复杂度是 $O(n\log n)$ 的，注意需要分别预处理正着和倒着的哈希值。

记 $ans_i$ 为以 $i$ 结尾的最长回文子串的长度，考虑 $ans_i\leq ans_{i-1}+2$ ，如果不合法就暴力向下递减。不难发现这个值是线性变化的，所以暴力最多要跑 $2n$ 次，总时间复杂度为 $O(n)$ 。

最长公共前缀

二分 + 哈希，二分前缀长度即可。

例题

P4824

维护一个栈，每次计算哈希值，如果这个栈的后缀是违禁词，那么暴力删除即可，使用 $O(1)$ 哈希比较。

// Problem: P4824 [USACO15FEB] Censoring S
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4824
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-01 20:48:01
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
string s,x;
const int base1=11453,base2=29521,mod=998244353;
long long _1[1000001]={1};
unsigned long long _2[1000001]={1};
long long hash1[1000001],hx1[1000001];
unsigned long long hash2[1000001],hx2[1000001];
pair<int,int> gethash(int l,int r){
	return make_pair((hash1[r]%mod-_1[r-l+1]*hash1[l-1]%mod+mod)%mod,
	hash2[r]-_2[r-l+1]*hash2[l-1]);
}
int f[1000001],ff[1000001];
deque<char> st;
int main(){
	ios::sync_with_stdio(0);
	for(int i=1;i<=1000000;i++)_1[i]=_1[i-1]*base1%mod,_2[i]=_2[i-1]*base2;
	cin>>s>>x;
	int sizx=x.size();
	hx1[0]=hx2[0]=x[0];
	for(int i=1;i<sizx;i++)hx1[i]=(hx1[i-1]*base1+x[i])%mod,hx2[i]=hx2[i-1]*base2+x[i];
	pair<int,int> P=make_pair(hx1[sizx-1],hx2[sizx-1]);
	int sizs=s.size();
	int top=0;
	for(int i=0;i<sizs;i++){
		top++;
		st.push_back(s[i]);
		hash1[top]=(hash1[top-1]*base1+s[i])%mod,hash2[top]=hash2[top-1]*base2+s[i];
		if(gethash(top-sizx+1,top)==P){
			top=top-sizx;
			for(int k=1;k<=sizx;k++)st.pop_back();
		}
	}
	while(!st.empty())cout<<st.front(),st.pop_front();
	return 0;
}

P3498

直接枚举 $k$ 然后计算即可。时间复杂度为 $O(\sum_{i=1}^n \left\lfloor\frac{n}{k}\right\rfloor)=O(n \ln n)$ 。

// Problem: P3498 [POI2010] KOR-Beads
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3498
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-02 08:20:24
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
const int base1=99887,base2=32997;
const int mod=998244353;
struct hash_pair{
	size_t operator()(const pair<long long ,unsigned long long> a)const {
		return ((a.first+a.second)*10001%mod+1007*a.first+10007*a.second)%mod;
	}
};
unordered_set<pair<long long ,unsigned long long>,hash_pair> s;
long long hash1[200001],hx1[200005];
unsigned long long hash2[200001],hx2[200005];
long long _1[200001]={1};
unsigned long long _2[200001]={1};
vector<int> A[200001];
int ans;
int n,a[200001];
pair<long long,unsigned long long> gethash(int l,int r){
	return make_pair(((hash1[r]-hash1[l-1]*_1[r-l+1]%mod)%mod+mod)%mod,
	hash2[r]-hash2[l-1]*_2[r-l+1]);
}
pair<long long,unsigned long long> _gethash(int l,int r){
	return make_pair(((hx1[l]-hx1[r+1]*_1[r-l+1]%mod)%mod+mod)%mod,
	hx2[l]-hx2[r+1]*_2[r-l+1]);
}
int main(){
	ios::sync_with_stdio(0);
	for(int i=1;i<=200000;i++)_1[i]=_1[i-1]*base1%mod,_2[i]=_2[i-1]*base2;
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int i=1;i<=n;i++){
		hash1[i]=(hash1[i-1]*base1%mod+a[i])%mod;
		hash2[i]=hash2[i-1]*base2+a[i];
	}
	for(int i=n;i>=1;i--){
		hx1[i]=(hx1[i+1]*base1%mod+a[i])%mod;
		hx2[i]=hx2[i+1]*base2+a[i];
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j*i<=n;j++){
			if(s.count(_gethash((j-1)*i+1,j*i)))continue;
			s.insert(gethash((j-1)*i+1,j*i));
		}
		int siz=s.size();
		A[siz].push_back(i);
		ans=max(ans,siz);
		s.clear();
	}
	cout<<ans<<" "<<A[ans].size()<<"\n";
	for(auto p:A[ans])cout<<p<<" ";
	return 0;
}

P3538

考虑判定循环节长度是否合法就是比较 $[l+len,r]$ 与 $[l,r-len]$ 哈希值是否相等。分解质因数后进行判定，若当前除去质因子后合法，那么保留该次除去的影响，直到找到最小解，这样可以做到 $O(q\log n)$ 。

下面是未加快读版：

// Problem: P3538 [POI2012] OKR-A Horrible Poem
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3538
// Memory Limit: 128 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-02 09:49:23
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
const int base=277;
unsigned long long _[500001]={1};
unsigned long long hsh[500001];
int n,m;
char c;
unsigned long long gethash(int l,int r){
	return hsh[r]-hsh[l-1]*_[r-l+1];
}
int prim[100001],pcnt,isp[500001];
void prework(){
	for(int i=2;i<=500000;i++){
		if(!isp[i])prim[++pcnt]=i,isp[i]=i;
		for(int j=1;j<=pcnt&&prim[j]*i<=500000;j++){
			isp[prim[j]*i]=prim[j];
			if(i%prim[j]==0)break;
		}
	}
}
int main(){
	ios::sync_with_stdio(0);
	cin>>n;
	for(int i=1;i<=n;i++)_[i]=_[i-1]*base;
	for(int i=1;i<=n;i++){
		cin>>c;
		hsh[i]=hsh[i-1]*base+c;
	}
	cin>>m;
	int x,y;
	prework();
	while(m--){
		cin>>x>>y;
		int len=y-x+1;
		int buf=len;
		while(buf!=1){
			// cout<<buf<<"\n";
			int pr=len/isp[buf];
			if(gethash(x+pr,y)==gethash(x,y-pr))len=pr;
			buf/=isp[buf];
		}
		cout<<len<<"\n";
	}
	return 0;
}

P4398

二维哈希，类比二维前缀和做即可。通用的方法是先用 base1 算出横向哈希，再用 base2 算出纵向哈希值（这里是前缀和形式）。具体可见代码。

这道题要二分矩形边长，用 unordered_set 维护哈希值是否出现。

// Problem: P4398 [JSOI2008] Blue Mary的战役地图
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4398
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-02 11:05:51
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
const int base1=277,base2=921;
unsigned long long hsh[1001][1001],hx[1001][1001];
unsigned long long _1[1001]={1},_2[1001]={1};
unsigned long long gethsh(int X1,int Y1,int X2,int Y2){
	return hsh[X2][Y2]-hsh[X2][Y1-1]*_1[Y2-Y1+1]-
	hsh[X1-1][Y2]*_2[X2-X1+1]+hsh[X1-1][Y1-1]*_1[Y2-Y1+1]*_2[X2-X1+1];
}
unsigned long long gethx(int X1,int Y1,int X2,int Y2){
	return hx[X2][Y2]-hx[X2][Y1-1]*_1[Y2-Y1+1]-
	hx[X1-1][Y2]*_2[X2-X1+1]+hx[X1-1][Y1-1]*_1[Y2-Y1+1]*_2[X2-X1+1];
}
unordered_set<unsigned long long> s;
int a[1001][1001],b[1001][1001];
int n;
bool check(int x){
	s.clear();
	for(int i=x;i<=n;i++){
		for(int j=x;j<=n;j++){
			s.insert(gethsh(i-x+1,j-x+1,i,j));
		}
	}
	for(int i=x;i<=n;i++){
		for(int j=x;j<=n;j++){
			if(s.count(gethx(i-x+1,j-x+1,i,j)))return 1;
		}
	}
	return 0;
}
int main(){
	ios::sync_with_stdio(0);
	cin>>n;
	for(int i=1;i<=n;i++)_1[i]=base1*_1[i-1],_2[i]=base2*_2[i-1];
	for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)cin>>a[i][j];
	for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)cin>>b[i][j];
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			hsh[i][j]=hsh[i][j-1]*base1+a[i][j];
			hx[i][j]=hx[i][j-1]*base1+b[i][j];
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			hsh[i][j]+=hsh[i-1][j]*base2;//两个维度必须分开预处理！！！
			hx[i][j]+=hx[i-1][j]*base2;
		}
	}
	int l=1,r=n,ans=0;
	while(l<=r){
		int mid=(l+r)/2;
		if(check(mid))ans=mid,l=mid+1;
		else r=mid-1;
	}
	cout<<ans;
	return 0;
}

P2601

枚举对称正方形的中心，进行二分，二分出最远的满足条件的地方并统计答案。

要维护三个不同方向的哈希值。

// Problem: P2601 [ZJOI2009] 对称的正方形
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2601
// Memory Limit: 128 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-02 11:51:52
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
const int base1=599,base2=971;
unsigned long long hsh1[1005][1005],hsh2[1005][1005],hsh3[1005][1005];
unsigned long long _1[1001]={1},_2[1001]={1};
unsigned long long gethash1(int X1,int Y1,int X2,int Y2){
	return hsh1[X2][Y2]-hsh1[X2][Y1-1]*_1[Y2-Y1+1]
	-hsh1[X1-1][Y2]*_2[X2-X1+1]
	+hsh1[X1-1][Y1-1]*_1[Y2-Y1+1]*_2[X2-X1+1];
}
unsigned long long gethash2(int X1,int Y1,int X2,int Y2){
	return hsh2[X1][Y2]-hsh2[X1][Y1-1]*_1[Y2-Y1+1]
	-hsh2[X2+1][Y2]*_2[X2-X1+1]
	+hsh2[X2+1][Y1-1]*_1[Y2-Y1+1]*_2[X2-X1+1];
}
unsigned long long gethash3(int X1,int Y1,int X2,int Y2){
	return hsh3[X2][Y1]-hsh3[X2][Y2+1]*_1[Y2-Y1+1]
	-hsh3[X1-1][Y1]*_2[X2-X1+1]
	+hsh3[X1-1][Y2+1]*_1[Y2-Y1+1]*_2[X2-X1+1];
}
int a[1001][1001];
int n,m;
bool check(int X1,int Y1,int X2,int Y2){
	return gethash1(X1,Y1,X2,Y2)==gethash2(X1,Y1,X2,Y2)&&gethash1(X1,Y1,X2,Y2)==gethash3(X1,Y1,X2,Y2);
}
int main(){
	ios::sync_with_stdio(0);
	cin>>n>>m;
	for(int i=1;i<=1000;i++)_1[i]=_1[i-1]*base1,_2[i]=_2[i-1]*base2;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>a[i][j];
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			hsh1[i][j]=hsh1[i][j-1]*base1+a[i][j];
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			hsh1[i][j]+=hsh1[i-1][j]*base2;
		}
	}
	for(int i=n;i>=1;i--){
		for(int j=1;j<=m;j++){
			hsh2[i][j]=hsh2[i][j-1]*base1+a[i][j];
		}
	}
	for(int i=n;i>=1;i--){
		for(int j=1;j<=m;j++){
			hsh2[i][j]+=hsh2[i+1][j]*base2;
			// if(j==1)cout<<hsh2[i][j]-hsh2[i+1][j]*base2<<"\n";
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=m;j>=1;j--){
			hsh3[i][j]=hsh3[i][j+1]*base1+a[i][j];
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=m;j>=1;j--){
			hsh3[i][j]+=hsh3[i-1][j]*base2;
		}
	}
	long long ans=0;
	// cout<<check(1,1,1,1)<<" "<<gethash1(1,1,1,1)<<" "<<gethash2(1,1,1,1)<<" "<<hsh2[4][1]-hsh2[5][1]*base2<<"\n";
	/*Deal with odd situations*/
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			int nowans=0;
			int l=1,r=min(min(n-i+1,i),min(m-j+1,j));
			while(l<=r){
				int mid=(l+r)/2;
				if(check(i-mid+1,j-mid+1,i+mid-1,j+mid-1))nowans=mid,l=mid+1;
				else r=mid-1;
			}
			// cout<<nowans<<" ";
			ans+=nowans;
		}
		// cout<<"\n";
	}
	/*Deal with even situations*/
	for(int i=1;i<n;i++){
		for(int j=1;j<m;j++){
			int nowans=0;
			int l=1,r=min(min(n-i,i),min(m-j,j));
			while(l<=r){
				int mid=(l+r)/2;
				if(check(i-mid+1,j-mid+1,i+mid,j+mid))nowans=mid,l=mid+1;
				else r=mid-1;
			}
			ans+=nowans;
		}
	}
	cout<<ans;
	return 0;
}

SP4103

暴力用哈希长度从大到小查找最长回文后缀即可。

// Problem: Extend to Palindrome
// Contest: SPOJ - Classical
// URL: https://www.spoj.com/problems/EPALIN/
// Memory Limit: 1536 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-02 15:42:17
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
const int base=1001;
unsigned long long hsh[100001],_hsh[100005];
unsigned long long _[100001]={1};
char s[100001];
unsigned long long gethash(int l,int r){
	return hsh[r]-hsh[l-1]*_[r-l+1];
}
unsigned long long _gethash(int l,int r){
	return _hsh[l]-_hsh[r+1]*_[r-l+1];
}
int ed;
bool check(int x){
	return gethash(ed-x+1,ed-x+x/2)==_gethash(ed-x/2+1,ed);
}
void clear(){
	for(int i=1;i<=ed;i++)s[i]=hsh[i]=_hsh[i]=0;
	return;
}
int main(){
	ios::sync_with_stdio(0);
	for(int i=1;i<=100000;i++)_[i]=_[i-1]*base;
	while(cin>>(s+1)){
		ed=strlen(s+1);
		// cout<<ed<<"\n";
		// int l=1,r=ed;
		for(int i=1;i<=ed;i++)hsh[i]=hsh[i-1]*base+s[i];
		for(int i=ed;i>=1;i--)_hsh[i]=_hsh[i+1]*base+s[i];
		int nowans=1;
		for(nowans=ed;nowans>=1;nowans--){
			if(check(nowans))break;
		}
		for(int i=1;i<=ed-(nowans+1)/2;i++)cout<<s[i];
		if(nowans&1)cout<<s[ed-(nowans+1)/2+1];
		for(int i=ed-(nowans+1)/2;i>=1;i--)cout<<s[i];
		cout<<"\n";
	}
	return 0;
}

P3167

考虑枚举每个通配符出现的位置，枚举每个通配符后面的一串字符，暴力用哈希 $O(1)$ 判断匹配，有如下 dp 方程式：

f_{i,j+len_i-1}=f_{i-1,j-2}\ (op_i=?) \\f_{i,j+len_i-1}=\max_{k=1}^jf_{i-1,k}\ (op_i=*)

暴力转移 + 哈希判断子串匹配即可。

// Problem: P3167 [CQOI2014] 通配符匹配
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3167
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-04 14:28:37
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int tpf[11],len[11],st,tcnt;
string s;
string t;
int ssiz,tsiz;
int n;
const int base=359;
unsigned long long hsh[100001],hx[100001];
unsigned long long _[100001]={1};
bool f[11][100005];
char tt[11];
int minn;
unsigned long long gethasho(int l,int r){
	return hsh[r]-hsh[l-1]*_[r-l+1];
}
unsigned long long gethasht(int l,int r){
	return hx[r]-hx[l-1]*_[r-l+1];
}
bool check(int le,int st1,int st2){
	if(le<1)return 1;
	else if(st1+le-1>tsiz||st2+le-1>ssiz)return 0;
	else return /*cerr<<gethasho(st1,st1+le-1)<<" "<<gethasht(st2,st2+le-1)<<"\n",*/gethasho(st2,st2+le-1)==gethasht(st1,st1+le-1);
}
int main(){
	ios::sync_with_stdio(0);
	cin>>s;
	ssiz=s.size();
	s=' '+s;
	for(int i=1;i<=ssiz;i++)hsh[i]=hsh[i-1]*base+s[i];
	for(int i=1;i<=100000;i++)_[i]=_[i-1]*base;
	for(int i=1;i<=ssiz;i++){
		if(s[i]=='*'||s[i]=='?')tpf[++tcnt]=i,tt[tcnt]=s[i],len[tcnt-1]=tpf[tcnt]-tpf[tcnt-1]-1;
	}
	len[tcnt]=ssiz-tpf[tcnt];
	st=tpf[1];
	cin>>n;
	while(n--){
		cin>>t;
		tsiz=t.size();
		t=' '+t;
		for(int i=1;i<=tsiz;i++)hx[i]=hx[i-1]*base+t[i];
		if(!check(st-1,1,1)){
			cout<<"NO\n";
			continue;
		}
		// cerr<<st<<" "<<n+1<<" remaining , now start\n";
		f[0][st-1]=1;
		for(int i=1;i<=tcnt;i++){
			// cerr<<i<<" "<<tt[i]<<"\n";
			if(tt[i]=='*'){
				int j=1;
				for(j=0;j<=tsiz;j++)if(f[i-1][j])break;
				if(j==tsiz+1)continue;
				// cerr<<len[i]<<" "<<j<<" "<<tpf[i]<<" "<<check(3,1,2)<<"\n";
				if(len[i]==0){
					for(;j<=tsiz;j++)f[i][j]=1;
				}
				else for(j++;j<=tsiz;j++){
					if(check(len[i],j,tpf[i]+1))f[i][j+len[i]-1]=1;//,cout<<j+len[i]-1<<"\n";
				}
			}
			else{
				for(int j=1;j<=tsiz;j++){
					if(f[i-1][j-1]&&check(len[i],j+1,tpf[i]+1))f[i][j+len[i]]=1;
				}
			}
		}
		if(f[tcnt][tsiz])cout<<"YES\n";
		else cout<<"NO\n";
		for(int i=1;i<=tcnt;i++)for(int j=0;j<=tsiz;j++)f[i][j]=0;
	}
	return 0;
}

注意要特殊关注一下几个通配符挤在一起的情况，因为这个时候接在后面的子串长度 $len_i=0$ 。

P3449

不难发现，符合条件的二元组 $(a,b)$ 满足 $a$ 是 $b$ 的前缀且 $b$ 除去 $a$ 的部分仍是回文串。前者用 Trie 维护，后者哈希判断，最后只在 Trie 上加能产生贡献的点，最后每个字符串逐一进行贡献的询问即可。设此时答案为 $ans$ ，那么最终答案即为 $ans\times 2+n$ ，因为当满足贡献时，原串被分成两部分回文串，二元组中元素可以互换。而原串为回文串，那么自己接自己一定有贡献。

// Problem: P3449 [POI2006] PAL-Palindromes
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3449
// Memory Limit: 375 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-04 18:03:30
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
unsigned long long hsh[2000005],hx[2000005];
const int base=277;
unsigned long long _[2000005]={1};
unsigned long long gethash1(int l,int r){
	return hsh[r]-hsh[l-1]*_[r-l+1];
}
unsigned long long gethash2(int l,int r){
	return hx[l]-hx[r+1]*_[r-l+1];
}
bool chkpalin(int len,int ed){
	return gethash1(ed-len/2+1,ed)==gethash2(ed-len+1,ed-len+len/2);
}
bool W[2000005],*w[2000005];
char S[2000005],*s[2000005];
int ch[2000005][26],cnt[2000005],now,len[2000005],tot;
void insert(int id,int now=0){
	for(int o=0;o<len[id];o++){
		int nxt=(ch[now][s[id][o]-'a']?ch[now][s[id][o]-'a']:ch[now][s[id][o]-'a']=++tot);
		cnt[nxt]+=w[id][o];
		now=nxt;
	}
	return;
}
int calc(int id,int now=0){
	for(int o=0;o<len[id];o++){
		now=ch[now][s[id][o]-'a'];
	}
	return cnt[now];
}
int n;
int main(){
	ios::sync_with_stdio(0);
	for(int i=1;i<=200000;i++)_[i]=_[i-1]*base;
	cin>>n;
	s[1]=S,w[1]=W;
	for(int i=1;i<=n;i++){
		// cerr<<i<<"\n";
		cin>>len[i];
		w[i+1]=w[i]+len[i];
		s[i+1]=s[i]+len[i];
		cin>>s[i];
		// cerr<<i<<"\n";
		hsh[0]=s[i][0];
		for(int j=1;j<len[i];j++)hsh[j]=hsh[j-1]*base+s[i][j];
		// hx[len[i]]=0;
		for(int j=len[i]-1;j>=1;j--)hx[j]=hx[j+1]*base+s[i][j];
		// w[i][len[i]-1]
		for(int L=1;L<len[i];L++)w[i][len[i]-L-1]=chkpalin(L,len[i]-1);//,cerr<<L<<"\n";;
		// cerr<<i<<"\n";
		insert(i);
	}
	long long ans=0;
	for(int i=1;i<=n;i++)ans+=calc(i);
	cout<<ans*2+n;
	return 0;
}

CF504E

在树上二分前缀长度即可。

这题非常毒瘤，不想多说了，主要就是把路径分成 $3$ 大段来求解二分区间，然后直接二分找到答案。

// Problem: Misha and LCP on Tree
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF504E
// Memory Limit: 500 MB
// Time Limit: 8000 ms
// Start coding at 2023-12-04 19:30:24
// 
// Powered by CP Editor (https://cpeditor.org)
#pragma GCC optimize(2)
#pragma GCC optimize("Ofast")
#include<bits/stdc++.h>
using namespace std;
int n,m;
struct line{
	int to,link;
}E[600001];
int head[300005],tot;
void addE(int u,int v){
	E[++tot].link=head[u];
	E[tot].to=v;
	head[u]=tot;
	return;
}
const int base1=277,base2=487,mod=998244353;
long long ksm(long long a,long long b){
	if(b==0)return 1;
	if(b==1)return a;
	return (b&1?a:1)*ksm(a*a%mod,b/2)%mod;
}
long long _1[300005]={1},_2[300005]={1},i1[300005],i2[300005];
long long hsh1[300005],hsh2[300005];
long long hx1[300005],hx2[300005];
char w[300005];
int dep[300005],siz[300005],fa[300005][21],lson[300005];
int maxdep[300005];
void dfs1(int now,int f){
	hsh1[now]=(hsh1[f]*base1+w[now-1])%mod;
	hsh2[now]=(hsh2[f]*base2+w[now-1])%mod;
	hx1[now]=(hx1[f]+_1[dep[now]]*w[now-1])%mod;
	hx2[now]=(hx2[f]+_2[dep[now]]*w[now-1])%mod;
	fa[now][0]=f;
	siz[now]=1;
	for(int i=0;fa[now][i];)i++,fa[now][i]=fa[fa[now][i-1]][i-1];
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==f)continue;
		maxdep[E[i].to]=dep[E[i].to]=dep[now]+1;
		dfs1(E[i].to,now);
		siz[now]+=siz[E[i].to];
		maxdep[now]=max(maxdep[now],maxdep[E[i].to]);
		if(maxdep[E[i].to]>maxdep[lson[now]])lson[now]=E[i].to;
	}
	return;
}
int dfn[300005],dfncnt,rk[300005],L[300005],R[300005],RK[600005],rkcnt;
int ltop[300005],llen[300005];
vector<int> v[300005];
void dfs2(int now,int top){
	dfn[now]=++dfncnt;
	rk[dfncnt]=now;
	ltop[now]=top;
	L[now]=++rkcnt;
	RK[rkcnt]=now;
	llen[top]=max(dep[now]-dep[top]+1,llen[top]);
	if(lson[now])dfs2(lson[now],top),RK[++rkcnt]=now;
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==fa[now][0]||E[i].to==lson[now])continue;
		dfs2(E[i].to,E[i].to);
		RK[++rkcnt]=now;
	}
	if(now==top){
		v[now].push_back(now);
		for(int i=1;i<=llen[now];i++){
			v[now].push_back(fa[v[now][i-1]][0]);
		}
	}
	R[now]=rkcnt;
	return;
}
int lg[600005];
int kth(int now,int k){
	if(k==0)return now;
	// exit(0);
	int o=lg[k];
	// exit(0);
	now=fa[now][o];
	// exit(0);
	k=k-(1<<o);
	// cerr<<k-(dfn[now]-dfn[ltop[now]])<<" "<<v[ltop[now]].size();
	// if(k-(dfn[now]-dfn[ltop[now]])>=(int)v[ltop[now]].size())cout<<now<<" "<<dfn[now]<<" "<<dfn[ltop[now]]<<" "<<ltop[now]<<" "<<k-(dfn[now]-dfn[ltop[now]])<<" "<<v[ltop[now]].size()<<" "<<v[ltop[now]][v[ltop[now]].size()-1]<<" "<<(1<<o)<<" in\n",exit(0);
	// exit(0);
	// cerr<<"\n"<<now<<" "<<k<<" "<<dfn[now]-dfn[ltop[now]]<<" in kth\n";
	if(dfn[now]-dfn[ltop[now]]>=k)return rk[dfn[now]-k];
	else return /*cout<<2<<" hanghang\n",*/v[ltop[now]][k-(dfn[now]-dfn[ltop[now]])];
}
int st[600005][21];
int seq[600005];
void lcainit(){
	for(int i=1;i<=rkcnt;i++){
		st[i][0]=dep[RK[i]];
	}
	for(int o=1;o<=20;o++)
		for(int i=1;i<=rkcnt-(1<<(o))+1;i++){
			st[i][o]=min(st[i][o-1],st[i+(1<<(o-1))][o-1]);
		}
	return;
}
int lca(int u,int v){
	// if(dfn[u]>dfn[v])swap(u,v);
	// if(L[u]<L[v]&&R[v]<R[u])return u;
	// cerr<<u<<" "<<v<<"\n";
	int ll=min(L[u],L[v]),rr=max(R[u],R[v]);
	int cha=rr-ll+1;
	// if(lg[cha]>=20)cout<<lg[cha]<<"\n";
	// cerr<<cha<<" "<<ll<<" "<<rr-(1<<lg[cha])+1<<" "<<st[ll][lg[cha]]<<"\n";
	return kth(u,dep[u]-min(st[ll][lg[cha]],st[rr-(1<<lg[cha])+1][lg[cha]]));
}
// int lca(int u,int v){
	// if(dep[u]>dep[v])swap(u,v);
	// for(int i=dep[v]-dep[u],ci=0;i;i>>=1,ci++)if(i&1)v=fa[v][ci];
	// if(u==v)return v;
	// for(int i=19;i>=0;i--)if(fa[u][i]!=fa[v][i])u=fa[u][i],v=fa[v][i];
	// return fa[u][0];
// }
int a,b,c,d;
pair<long long,long long> uphash(int u,int v){
	return make_pair(((hx1[u]-hx1[fa[v][0]]+mod)*i1[dep[v]])%mod,
	((hx2[u]-hx2[fa[v][0]]+mod)*i2[dep[v]])%mod);
}
pair<long long,long long> downhash(int u,int v){
	return make_pair(((hsh1[v]-hsh1[fa[u][0]]*_1[dep[v]-dep[u]+1])%mod+mod)%mod,
	((hsh2[v]-hsh2[fa[u][0]]*_2[dep[v]-dep[u]+1])%mod+mod)%mod);
}

int main(){
	ios::sync_with_stdio(0);
	for(int i=2;i<=600000;i++)lg[i]=lg[i/2]+1;
	// cout<<lg[600000];
	i1[0]=1;
	i2[0]=1;
	for(int i=1;i<=300000;i++)_1[i]=_1[i-1]*base1%mod,_2[i]=_2[i-1]*base2%mod,i1[i]=ksm(_1[i],mod-2),i2[i]=ksm(_2[i],mod-2);
	cin>>n;
	cin>>w;
	int x,y;
	for(int i=1;i<n;i++)cin>>x>>y,addE(x,y),addE(y,x);
	// return 0;
	cin>>m;
	dfs1(1,0);
	dfs2(1,1);
	lcainit();
	// if(n==300000&&w[0]=='c')cout<<rkcnt<<"\n";
	// dep[0]=-1;
	// return 0;
	while(m--){
		cin>>a>>b>>c>>d;
		int lca1=lca(a,b);
		int lca2=lca(c,d);
		// return 0;
		int l1=dep[a]-dep[lca1],l2=dep[c]-dep[lca2];
		if(l1>l2){
			swap(a,c);
			swap(b,d);
			swap(lca1,lca2);
			swap(l1,l2);
		}
		int ans=0;
		// cerr<<a<<" "<<b<<" "<<c<<" "<<d<<" "<<lca1<<" "<<lca2<<" "<<dep[a]<<"\n";
		pair<long long,long long> p1=uphash(a,lca1),p2=uphash(c,kth(c,dep[a]-dep[lca1]));
		// cerr<<p1.first<<" "<<p2.first<<" "<<hx1[0]<<" "<<hx1[1]<<" "<<uphash(1,1).first<<"\n";
		// return 0;
		if(p1==p2){
			// cerr<<"in 1\n";
			if(dep[a]+dep[b]-2*dep[lca1]<dep[c]-dep[lca2])p1=make_pair(-1,-1);
			else p1=downhash(lca1,kth(b,dep[a]+dep[b]-2*dep[lca1]-(dep[c]-dep[lca2])));
			p2=uphash(kth(c,dep[a]-dep[lca1]),lca2);
			// cerr<<"over chk 1\n";
			if(p1==p2){
				// cerr<<"in 2\n";
				ans=dep[c]-dep[lca2]+1;
				int st=dep[a]+dep[b]-2*dep[lca1]-(dep[c]-dep[lca2]);
				int res=0,l=1,r=min(st,dep[d]-dep[lca2]);
				// cerr<<st<<" "<<kth(5,1)<<"\n";
				// cerr<<kth(b,st)<<" "<<kth(b,st-1)<<" "<<lca2<<" "<<kth(d,dep[d]-dep[lca2]-1)<<"\n";
				while(l<=r){
					int mid=(l+r)/2;
					if(downhash(kth(b,st),kth(b,st-mid))==downhash(lca2,kth(d,dep[d]-dep[lca2]-mid)))res=mid,l=mid+1;
					else r=mid-1;
				}
				ans+=res;
				cout<<ans<<"\n";
			}else{
				ans=dep[a]-dep[lca1]+1;
				int st=dep[b]-dep[lca1];
				int res=0,l=1,r=min(dep[b]-dep[lca1],dep[c]-dep[lca2]-(dep[a]-dep[lca1]));
				while(l<=r){
					int mid=(l+r)/2;
					if(downhash(kth(b,st),kth(b,st-mid))==uphash(kth(c,dep[a]-dep[lca1]),kth(c,dep[a]-dep[lca1]+mid)))res=mid,l=mid+1;
					else r=mid-1;
				}
				ans+=res;
				cout<<ans<<"\n";
			}
		}else{
			int l=0,r=dep[a]-dep[lca1];
			while(l<=r){
				int mid=(l+r)/2;
				if(uphash(a,kth(a,mid))==uphash(c,kth(c,mid)))ans=mid+1,l=mid+1;
				else r=mid-1;
			}
			cout<<ans<<"\n";
		}
	}
	return 0;
}

P9576

考虑把问题简化成选择 $[l_1,r_1]$ 和 $[l_2,r_2]$ 区间的字符串拼在一起，使得拼完之后的串为 $t$ ，因为原问题中把一个区间的字符串与 $t$ 完全匹配的答案是好求的。

考虑计算每个点为起点与 $t$ 的最长公共前缀和每个点为终点与 $t$ 的最长公共后缀。二分 + 哈希即可，然后特判完全匹配的串，把它当做只差一个字符匹配的串，并晚加贡献，那么贡献就是 $pre_i+suf_j-|t|+1$ ，使用线段树维护。不难发现上面式子有限制 $i\leq j-|t|$ ，从 $tsiz$ 处开始扫一遍即可。

// Problem: P9576 「TAOI-2」Ciallo～(∠・ω< )⌒★
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P9576
// Memory Limit: 512 MB
// Time Limit: 2000 ms
// Start coding at 2023-12-05 15:36:31
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
#define int long long
using namespace std;
unsigned long long hsh1[400005],hsh2[200005];
const int base=279;
unsigned long long _[400005]={1};
char s[400005],t[200005];
int tsiz,ssiz;
unsigned long long gethash1(int l,int r){
	return hsh1[r]-hsh1[l-1]*_[r-l+1];
}
unsigned long long gethash2(int l,int r){
	return hsh2[r]-hsh2[l-1]*_[r-l+1];
}
bool check(int len,int st1,int st2){
	if(len<1)return 1;
	else if(st1+len-1>ssiz||st2+len-1>tsiz)return 0;
	else return gethash1(st1,st1+len-1)==gethash2(st2,st2+len-1);
}
int pre[400005],suf[400005];
int xds[1600005],cnt[1600005];
void pushup(int now){
	xds[now]=xds[now<<1]+xds[now<<1|1];
	cnt[now]=cnt[now<<1]+cnt[now<<1|1];
	return;
}
void mdf(int now,int l,int r,int q){
	if(l==r)return xds[now]+=q,cnt[now]++,void();
	int mid=(l+r)/2;
	if(q<=mid)mdf(now<<1,l,mid,q);
	else mdf(now<<1|1,mid+1,r,q);
	pushup(now);
}
pair<int,int> operator + (const pair<int,int> a,const pair<int,int> b){
	return make_pair(a.first+b.first,a.second+b.second);
}
pair<int,int> qsum(int now,int l,int r,int sl,int sr){
	if(l==sl&&r==sr)return make_pair(xds[now],cnt[now]);
	int mid=(l+r)/2;
	pair<int,int> res=make_pair(0,0);
	if(sl<=mid)res=res+qsum(now<<1,l,mid,sl,min(sr,mid));
	if(sr>mid)res=res+qsum(now<<1|1,mid+1,r,max(sl,mid+1),sr);
	pushup(now);
	return res;
}
long long ans;
signed main(){
	ios::sync_with_stdio(0);
	cin>>s>>t;
	ssiz=strlen(s);
	tsiz=strlen(t);
	for(int i=1;i<=400000;i++)_[i]=_[i-1]*base;
	for(int i=1;i<=ssiz;i++)hsh1[i]=hsh1[i-1]*base+s[i-1];
	for(int i=1;i<=tsiz;i++)hsh2[i]=hsh2[i-1]*base+t[i-1];
	for(int i=1;i<=ssiz;i++){
		int l=0,r=min(ssiz-i+1,tsiz);
		while(l<=r){
			int mid=(l+r)/2;
			if(check(mid,i,1))pre[i]=mid,l=mid+1;
			else r=mid-1;
		}
		// cerr<<i<<" "<<pre[i]<<"\n";
	}
	for(int i=1;i<=ssiz;i++){
		int l=0,r=min(i,tsiz);
		while(l<=r){
			int mid=(l+r)/2;
			if(check(mid,i-mid+1,tsiz-mid+1))suf[i]=mid,l=mid+1;
			else r=mid-1;
		}
	}
	// return 0;
	for(int i=tsiz;i<=ssiz;i++){
		// cerr<<i<<" "<<pre[i]<<" "<<suf[i]<<" "<<ans<<"\n";
		if(pre[i-tsiz+1])if(suf[i]!=tsiz)mdf(1,1,tsiz,pre[i-tsiz+1]);
		if(suf[i]==tsiz)ans+=(i-tsiz)*(i-tsiz-1)/2+ssiz-tsiz+(ssiz-i)*(ssiz-i-1)/2;
		if(suf[i]!=0){
			int Q=tsiz-suf[i];
			if(suf[i]==tsiz)Q++;
			pair<int,int> res=qsum(1,1,tsiz,Q,tsiz);
			// cerr<<"in "<<res.first-res.second*(tsiz-suf[i]-1)<<"\n";
			ans+=res.first-res.second*(Q-1);
		}
		if(suf[i]==tsiz)mdf(1,1,tsiz,pre[i-tsiz+1]-1);
	}
	cout<<ans;
	return 0;
}

P5184

不难发现比较字典序可以使用二分 + 哈希的方式比较，找出最长前缀之后比较下一个字符即可。

注意不要把数组建在结构体内，这样复杂度就变成 $O(n^3)$ 了。

// Problem: P5184 [COCI2009-2010#2] PASIJANS
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5184
// Memory Limit: 125 MB
// Time Limit: 1500 ms
// Start coding at 2023-12-05 18:51:37
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
const int base=277;
unsigned long long _[1001]={1};
int num[1003][1003];
unsigned long long hsh[1003][1003];
struct seq{
	int l,r;
	int id;
	inline unsigned long long gethash(int L,int R)const{
		return hsh[R][id]-hsh[L-1][id]*_[R-L+1];
	}
};
bool operator < (const seq o,const seq a){
	int L=0,R=min(o.r-o.l+1,a.r-a.l+1);
	int res=0;
	while(L<=R){
		int mid=(L+R)/2;
		if(o.gethash(o.l,o.l+mid-1)==a.gethash(a.l,a.l+mid-1))res=mid,L=mid+1;
		else R=mid-1;
	}
	if(L>min(o.r-o.l+1,a.r-a.l+1))return o.r-o.l+1<a.r-a.l+1;
	else return num[o.l+res][o.id]>num[a.l+res][a.id];
}
priority_queue<seq> q;
int n,o;
seq temp;
int main(){
	ios::sync_with_stdio(0);
	for(int i=1;i<=1000;i++)_[i]=_[i-1]*base;
	cin>>n;
	int idcnt=0;
	while(n--){
		cin>>o;
		++idcnt;
		for(int i=1;i<=o;i++)cin>>num[i][idcnt];
		for(int i=1;i<=o;i++)hsh[i][idcnt]=hsh[i-1][idcnt]*base+num[i][idcnt];
		temp.l=1,temp.r=o,temp.id=idcnt;
		q.push(temp);
		//for(int i=1;i<=o;i++)temp.num[i]=temp.hsh[i]=0;
	}
	while(!q.empty()){
		temp=q.top();
		q.pop();
		temp.l++;
		cout<<num[temp.l-1][temp.id]<<" ";
		if(temp.l<=temp.r){
			q.push(temp);
		}
	}
	return 0;
}

完工！

哈希与自然根号

鸽。

KMP

其实 KMP 本身用于字符串匹配其实实用性价值不大，因为字符串哈希也能做到相同的复杂度。KMP 最有优势的地方是它能快速求出 $s$ 任意前缀的最长 border（既是一个串的真前缀又是一个串的真后缀）。

思想

考虑不难发现，我们假如说已经求出 $[1,k]$ 的所有最长 border 长度，而有一个数组记录了这些长度，考虑如何求出第 $k+1$ 位置的最长 border 长度。

假定字符串从 $0$ 开始。~~（虽然图是从 $1$ 开始的）~~

一个非常 trival 的想法是，最优情况下， $k+1$ 位置的 border 可以直接继承前面 $pi_k$ 的 border 长度，那么就只需要比较 $s_{pi_k}$ 与 $s_{k+1}$ 就行了？

是的。

但如果不匹配呢？

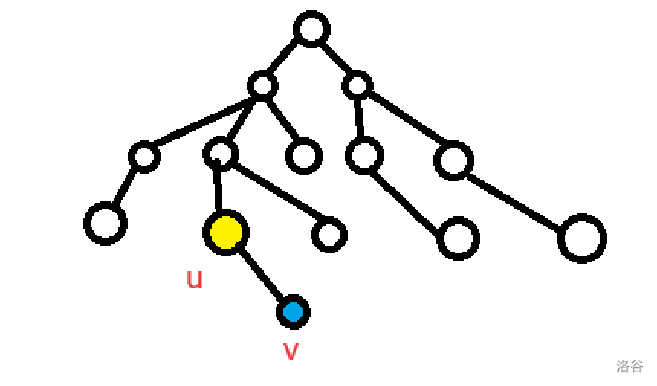
不难发现，图中绿色的部分就是 $[0,k]$ 的最长 border。

如果最长 border 不匹配怎么办？那就找次长 border 再来试试！

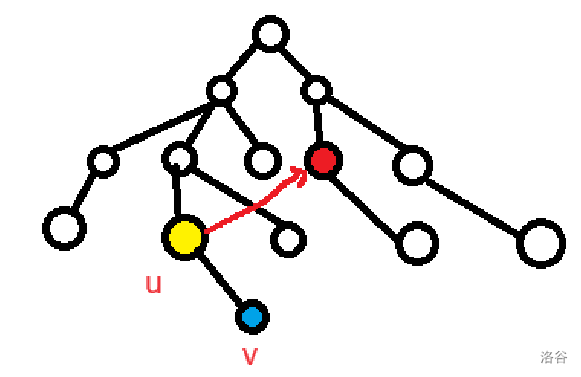
如何找到次长 border 呢？考虑次长 border 一定是左边绿色部分的真前缀，也是右边绿色部分的真后缀。而绿色部分是一样的！！！

所以我们得到了次长 border 是最长 border 的最长 border，也就是说第 $k$ 长 border 是第 $k-1$ 长 border 的最长 border。

那么暴力找到这些 border 然后一个一个看能不能与下一位 $s_{k+1}$ 匹配即可。

核心代码：

vector<int> pre_func(string s){
    int siz=s.size();
    vector<int> pi(siz);
    for(int i=1;i<siz;i++){
        int j=pi[i-1];
        while(j>0&&s[i]!=s[j])j=pi[j-1];
        if(s[i]==s[j])j++;
        pi[i]=j;
    }
    return pi;
}

应用

字符串的周期

不难发现， $p$ 为 $s$ 的周期 $\Leftrightarrow$ $s[1,n-p]$ 为 $s$ 的 border，有周期的长为 $n$ 的字符串的最短周期为 $n-next_n$ 。

失配树

根据上面的 KMP 思想的阐述，我们直接对于 $(pi_i,i)$ 加一条边，因为 $pi_i<i$ ，所以连出来的图就是一棵树。此时不难发现对于该树上的每一个节点 $i$ ，他的每一个祖先 $j$ 都满足 $[1,j]$ 是 $[1,i]$ 的 border。

该树被称作 失配树。

例题

P5829 【模板】失配树

考虑最长公共 border 一定满足是这两个前缀的 border，那么根据失配树的性质，建出失配树跑 LCA 就行了。

注意当 LCA 是这两个原来节点中的其中一个的时候，要输出它的父亲，因为一个字符串的 border 不能是他自己。

还要注意如果用树剖写的话要保证节点编号不为 $0$ 。

// Problem: P5829 【模板】失配树
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5829
// Memory Limit: 512 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-06 08:25:12
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int si;
vector<int> pre_func(string s){
	si=s.size();
	vector<int> pi(si);
	// pi[0]=0;
	for(int i=1;i<si;i++){
		int j=pi[i-1];
		while(j>0&&s[i]!=s[j])j=pi[j-1];
		if(s[i]==s[j])j++;
		pi[i]=j;
	}
	// cerr<<"11111\n";
	return pi;
}
string s;
int m,l,r;
struct line{
	int to,link;
}E[2000005];
int head[1000005],tot;
void addE(int u,int v){
	E[++tot].link=head[u];
	E[tot].to=v;
	head[u]=tot;
	// cout<<u<<" "<<v<<"\n";
	return;
}
int dep[1000005],siz[1000005],hson[1000005],fa[1000005];
void dfs1(int now,int f){
	fa[now]=f;
	siz[now]=1;
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==f)continue;
		dep[E[i].to]=dep[now]+1;
		dfs1(E[i].to,now);
		siz[now]+=siz[E[i].to];
		if(siz[hson[now]]<siz[E[i].to])hson[now]=E[i].to;
	}
	return;
}
int dfn[1000005],rk[1000005],dfncnt;
int ltop[1000005];
void dfs2(int now,int top){
	ltop[now]=top;
	dfn[now]=++dfncnt;
	rk[dfncnt]=now;
	if(!hson[now])return;
	dfs2(hson[now],top);
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==fa[now]||E[i].to==hson[now])continue;
		dfs2(E[i].to,E[i].to);
	}
	return;
}
int lca(int u,int v){
	while(ltop[u]!=ltop[v]){
		if(dep[ltop[u]]>dep[ltop[v]])u=fa[ltop[u]];
		else v=fa[ltop[v]];
	}
	return rk[min(dfn[u],dfn[v])];
}


int main(){
	ios::sync_with_stdio(0);
	cin>>s;
	vector<int> pi=pre_func(s);
	// cerr<<"\n?";
	for(int i=0;i<si;i++)addE(i+2,pi[i]+1),addE(pi[i]+1,i+2);
	int m,x,y;
	dfs1(1,0);
	dfs2(1,1);
	cin>>m;
	while(m--){
		cin>>x>>y;
		int lc=lca(x+1,y+1);
		if(lc==x+1||lc==y+1)lc=fa[lc];
		cout<<lc-1<<"\n";
	}
	return 0;
}

P2375 动物园

失配树上倍增找第一个不重叠的 border 就行了。

// Problem: P2375 [NOI2014] 动物园
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2375
// Memory Limit: 512 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-06 15:31:47
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
struct line{
	int to,link;
}E[2000001];
int head[1000005],tot;
int si,n;
vector<int> pre_func(string &s){
	si=s.size();
	vector<int> pi(si);
	for(int i=1;i<si;i++){
		int j=pi[i-1];
		while(j>0&&s[i]!=s[j])j=pi[j-1];
		if(s[i]==s[j])j++;
		pi[i]=j;
	}
	return pi;
}
string s;
void addE(int u,int v){
	E[++tot].link=head[u];
	E[tot].to=v;
	head[u]=tot;
	return;
}
int dep[1000005],siz[1000005],fa[1000005][21],mfd[1000005];
void clear(){
	for(int i=1;i<=si+2;i++)head[i]=0;
	// for(int i=1;i<=1000000;i++)for(int j=1;j<=20;j++)fa[i][j]=0;
	// for(int i=1;i<=tot;i++)E[i]={0,0};
	tot=0;
	return;
}
void dfs(int now,int f){
	fa[now][0]=f;
	siz[now]=1;
	int o;
	for(o=0;fa[now][o];)o++,fa[now][o]=fa[fa[now][o-1]][o-1];
	mfd[now]=o-1;
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==f)continue;
		dep[E[i].to]=dep[now]+1;
		dfs(E[i].to,now);
		siz[now]+=siz[E[i].to];
	}
	return;
}
int getans(int pos){
	int org=pos;
	for(int o=mfd[pos];o>=0;o--)if(fa[pos][o]-1>(org-1)/2)pos=fa[pos][o];
	// cout<<dep[fa[pos][0]]<<" hanghang shi xiachou\n";
	return dep[fa[pos][0]];
}
int main(){
	ios::sync_with_stdio(0);
	cin>>n;
	while(n--){
		clear();
		cin>>s;
		vector<int> pi=pre_func(s);
		for(int i=0;i<si;i++)addE(i+2,pi[i]+1),addE(pi[i]+1,i+2);
		dfs(1,0);
		long long ans=1;
		for(int i=2;i<=si+1;i++)ans*=(getans(i)+1),ans%=1000000007ll;
		cout<<ans<<"\n";
	}
	return 0;
}

CF526D

考虑合法时的前缀函数是怎样的。不难发现当一般情况时，前缀函数算出的一个类循环节段数 $len$ ，必定满足 $len/k> len\bmod k$ ，而当原串有循环节时，满足 $len/k>len\bmod k$ ，这个结论手玩一下 A 为空，B 为空，A/B=a/b $\times$ 循环节长度就能得到。

// Problem: Om Nom and Necklace
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF526D
// Memory Limit: 250 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-06 17:02:52
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int si;
vector<int> pre_func(string &s){
	si=s.size();
	vector<int> pi(si);
	for(int i=1;i<si;i++){
		int j=pi[i-1];
		while(j>0&&s[i]!=s[j])j=pi[j-1];
		if(s[i]==s[j])j++;
		pi[i]=j;
	}
	return pi;
}
string s;
int k;
int main(){
	ios::sync_with_stdio(0);
	cin>>k>>k;
	cin>>s;
	vector<int> pi=pre_func(s);
	for(int i=0;i<si;i++){
		int len=i-pi[i]+1;
		int cnt=(i+1)/len;
		if((i+1)%len)cout<<(cnt/k>cnt%k);
		else cout<<(cnt/k>=cnt%k);
	}
	return 0;
}

CF432D

手玩一下可以发现一个 border 在原串的出现次数就是失配树上该长度对应节点的子树大小。那么直接统计即可。

// Problem: Prefixes and Suffixes
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF432D
// Memory Limit: 250 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-06 20:09:29
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int si;
vector<int> pre_func(string &s){
	si=s.size();
	vector<int> pi(si);
	for(int i=1;i<si;i++){
		int j=pi[i-1];
		while(j>0&&s[i]!=s[j])j=pi[j-1];
		if(s[i]==s[j])j++;
		pi[i]=j;
	}
	return pi;
}
string s;
struct line{
	int to,link;
}E[200005];
int head[100005],tot;
void addE(int u,int v){
	E[++tot].link=head[u];
	E[tot].to=v;
	head[u]=tot;
	return;
}
int siz[100005],fa[100005],dep[100005];
void dfs(int now,int f){
	siz[now]=1;
	fa[now]=f;
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==f)continue;
		dep[E[i].to]=dep[now]+1;
		dfs(E[i].to,now);
		siz[now]+=siz[E[i].to];
	}
	return;
}
pair<int,int> ans[100005];
int main(){
	ios::sync_with_stdio(0);
	cin>>s;
	vector<int> pi=pre_func(s);
	for(int i=0;i<si;i++)addE(i+2,pi[i]+1),addE(pi[i]+1,i+2);
	dfs(1,0);
	int pos=si+1,cnt=dep[pos];
	while(pos!=1){
		ans[cnt--]=make_pair(pos-1,siz[pos]);
		pos=fa[pos];
	}
	cout<<dep[si+1]<<"\n";
	for(int i=1;i<=dep[si+1];i++)cout<<ans[i].first<<" "<<ans[i].second<<"\n";
	return 0;
}

P3435

考虑使用失配树。不难发现 最长周期 长度就是原字符串长度减其最小 border 的长度，放到失配树上，就是求一个节点在失配树上距离他最远的非根祖先。直接暴力 dfs 记录即可。

// Problem: P3435 [POI2006] OKR-Periods of Words
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3435
// Memory Limit: 128 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-06 20:49:40
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int si;
vector<int> pre_func(string &s){
	si=s.size();
	vector<int> pi(si);
	for(int i=1;i<si;i++){
		int j=pi[i-1];
		while(j>0&&s[i]!=s[j])j=pi[j-1];
		if(s[i]==s[j])j++;
		pi[i]=j;
	}
	return pi;
}
string s;
struct line{
	int to,link;
}E[2000005];
int head[1000005],tot;
void addE(int u,int v){
	E[++tot].link=head[u];
	E[tot].to=v;
	head[u]=tot;
	return;
}
int ff[1000005];
void init(int now,int f,int v){
	ff[now]=v;
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==f)continue;
		init(E[i].to,now,v);
	}
	return;
}
void dfs(){
	for(int i=head[1];i;i=E[i].link){
		init(E[i].to,1,E[i].to);
	}
	return;
}

int main(){
	ios::sync_with_stdio(0);
	cin>>si;
	cin>>s;
	vector<int> pi=pre_func(s);
	for(int i=0;i<si;i++)addE(i+2,pi[i]+1),addE(pi[i]+1,i+2);
	dfs();
	long long ans=0;
	for(int i=2;i<=si+1;i++)ans+=i-ff[i];
	cout<<ans;
	return 0;
}

exKMP

可以在线性时间内跑出一个串的每个后缀和本身的最长前缀长度（即 $z$ 数组），通常用于优化 dp，但是很少有题会卡哈希 + 二分。

思想

思想和 KMP 本质差不多，就是用现在已有的信息优化求出剩下的信息。

加入我们现在已经求出 $z[0\cdots i]$ 了，我们来想如何用前面的信息求出 $z[i+1]$ 。

我们称上一次匹配的区间为 Z-box，显然，如果目前 $i+1>r$ ，那么这个点与之前的所有的比较都无关，需要暴力跑出该点的 $z$ 值。

而 $i+1\leq r$ ，情况就不太一样了。

不难发现，此时的字符串是长成这样的。由于我们保证 $i+1>l$ ，所以有 $s[i+1\cdots r]=s[i+1-l\cdots r-l]$ 。

现在我们成功的把目标字符串的前缀转化到了一个我们已经求出 $z$ 的位置。考虑这个时候直接调用 $z[i+1-l]$ 就能得到此时的 $z$ 函数值。

这时要分两种情况。如果这时的 $z$ 值小于我们的字符串长度，那么当前的 $z$ 值就是原来的 $z$ 值。

而如果大于等于，我们就只能得到 $z[i+1]\geq z[i+1-l]$ 的信息。那么就把 $z[i+1]$ 暴力赋值成 $r-i$ 后继续跑暴力。

复杂度不会证明，应该是 $O(n)$ 的。

而如果要求其他串每个长度的后缀与原串的最长公共前缀，就要使用原串的 $z$ 函数值来计算新串的信息，过程与上面相似。

例题

P5410 【模板】扩展 KMP/exKMP（Z 函数）

模板题。

// Problem: P5410 【模板】扩展 KMP/exKMP（Z 函数）
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5410
// Memory Limit: 500 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-07 15:13:53
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int si;
vector<int> getZ(string &s){
	si=s.size();
	vector<int> z(si);
	z[0]=si;
	int zl=0,zr=0;
	for(int i=1;i<si;i++){
		int j=i;
		if(i<=zr){
			if(z[i-zl]<zr-i+1)z[i]=z[i-zl],j=0;
			else j+=zr-i+1;
		}
		if(j){
			while(s[j]==s[j-i]&&j<si)j++;
			z[i]=j-i;
		}
		if(i+z[i]-1>zr)zl=i,zr=i+z[i]-1;
	}
	return z;
}
vector<int> exZ(string &s,string &t){
	int ssi=s.size();
	vector<int> sz=getZ(s);
	si=t.size();
	vector<int> z(si);
	int zl=-1,zr=-1;
	for(int i=0;i<si;i++){
		int j=i;
		if(i<=zr){
			if(sz[i-zl]<zr-i+1)z[i]=sz[i-zl],j=-1;
			else j+=zr-i+1;
		}
		// cout<<i<<" "<<j<<"\n";
		if(j!=-1){
			while(j<si&&j<ssi+i&&t[j]==s[j-i])j++;
			z[i]=j-i;
		}
		if(i+z[i]-1>zr)zl=i,zr=i+z[i]-1;
	}
	return z;
}
int ssiz,tsiz;
string s,t;
int main(){
	ios::sync_with_stdio(0);
	cin>>t>>s;
	long long ans=0;
	vector<int> sz=getZ(s);
	for(int i=0;i<si;i++)ans^=1ll*(i+1)*(sz[i]+1);
	cout<<ans<<"\n";
	ans=0;
	vector<int> tz=exZ(s,t);
	for(int i=0;i<si;i++)ans^=1ll*(i+1)*(tz[i]+1);
	cout<<ans;
	return 0;
}

PKUSC2023 D1T1

这道题做法是口胡的。

题意是给你两个字符串 $S$ 和 $T$ ，对于把每个 $S_i$ 换成 $T_i$ 后求出 $S$ 的最长 border。

考虑首先 exKMP + hash，可以枚举每一个和前缀编辑距离只差 $1$ 或 $2$ 的后缀。注意只有一个不同时就直接改那个就行了，有两个不同时要保证这两个字符在原串的位置相同，这样可以算出修改之后的最长 border。

对于无效修改，直接 KMP 求出 border。跳 border 然后暴力赋值答案，注意要特判 $S_i=T_i$ 。

一些题

P3193

设 $g[i][j]$ 为当前匹配 $i$ 位之后再加一个字符变为匹配 $j$ 位的方案数，这个用 KMP 易求（不过 $m\leq20$ ，唐），那么有 dp 方程：

dp_{i,j}=\sum_{k=0}^{m-1}dp_{i-1,k}\times g_{k,j}

矩阵乘法优化即可，时间复杂度 $O(m^3\log n)$ 。

代码调试语句较多。

// Problem: P3193 [HNOI2008] GT考试
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3193
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-07 21:20:50
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int si;
vector<int> pre_func(string &s){
	si=s.size();
	vector<int> pi(si);
	for(int i=1;i<si;i++){
		int j=pi[i-1];
		while(j>0&&s[i]!=s[j])j=pi[j-1];
		if(s[i]==s[j])j++;
		pi[i]=j;
	}
	return pi;
}
int n,m,k;
string ss;
struct matrix{
	int s[21][21];
	void clear(){
		for(int i=0;i<=m;i++){
			for(int j=0;j<=m;j++){
				s[i][j]=0;
			}
		}
		return;
	}
	void I(){
		clear();
		for(int i=0;i<=m;i++){
			s[i][i]=1;
		}
		return;
	}
	void print(){
		cerr<<m<<" nima\n";
		for(int i=0;i<=m;i++){
			for(int j=0;j<=m;j++){
				cerr<<s[i][j]<<" ";
			}
			cerr<<"\n";
		}
		return;
	}
	matrix operator * (const matrix &a) const{
		// exit(0);
		matrix res;
		res.clear();
		// cerr<<k<<"\n";
		// // exit(0);
		// cerr<<m<<"\n";
		// for(int i=0;i<=m;i++){
			// for(int j=0;j<=m;j++){
				// cerr<<s[i][j]<<" ";
			// }
			// cerr<<"\n";
		// }
		// for(int i=0;i<=m;i++){
			// for(int j=0;j<=m;j++){
				// cerr<<a.s[i][j]<<" ";
			// }
			// cerr<<"\n";
		// }
		for(int i=0;i<=m;i++){
			for(int j=0;j<=m;j++){
				for(int o=0;o<=m;o++){
					// cerr<<k<<"\n";
					res.s[i][j]+=s[i][o]*a.s[o][j];
					res.s[i][j]%=k;
					// cerr<<k<<"\n";
				}
			}
		}
		// a.print();
		// res.print();
		// exit(0);
		return res;
	}
}dp,g;
matrix I;
matrix ksm(matrix a,int b){
	// cerr<<k<<"\n";
	if(b==0)return I;
	if(b==1)return a;
	// cerr<<"???\n";
	return (b&1?a:I)*ksm(a*a,b/2);
}
int cnt[10],anow=10;
int main(){
	ios::sync_with_stdio(0);
	cin>>n>>m>>k>>ss;
	// cout<<k<<"\n";
	I.I();
	vector<int> pi=pre_func(ss);
	for(int i=0;i<si-1;i++){
		// cout<<i+1<<"\n";
		anow=10;
		for(int i=0;i<=9;i++)cnt[i]=0;
		int pos=pi[i];
		g.s[i+1][i+2]=1,cnt[ss[i+1]-'0']++,anow--;
		// cout<<anow<<" "<<ss[i+1]-'0'<<"\n";
		while(pos>=0){
			// cout<<pos<<" ";
			if(!cnt[ss[pos]-'0'])g.s[i+1][pos+1]=1,cnt[ss[pos]-'0']++,anow--;//,cout<<ss[pi[pos]]-'0'<<"\n";
			if(pos<=0)break;
			pos=pi[pos-1];
		}
		// cout<<"\n"<<anow<<"\n\n";
		g.s[i+1][0]=anow;
	}
	g.s[0][1]=1;
	g.s[0][0]=9;
	g.s[m][0]=0;
	// g.s[m][m]=10;
	dp.s[0][0]=1;
	// g.print();
	dp=dp*ksm(g,n);
	// return 0;
	long long ans=0;
	for(int i=0;i<m;i++)ans+=dp.s[0][i];
	cout<<ans%k;
	return 0;
}

CF1051E

前缀和优化 dp。

不难发现可以列出一个这样的 dp 方程式：

dp_i=\sum_{j=len_l}^{len_r}dp_{i-j}\times[l\leq \operatorname{atoi}(s[i-j+1\cdots i])\leq r]\times[s[i-j+1]\not=0]

其中 $j\in[len_l+1,len_r-1]$ 中的情况可以直接累加，使用前缀和 $O(1)$ 转移，我们要判断的是在边界时的划分出的数与 $l$ 与 $r$ 的大小关系。

使用哈希 + 二分可以做到 $O(n\log n)$ ，但是对 $l$ 与 $r$ 求解 Z 函数可以做到 $O(n)$ 。

代码待补。

border 理论与均摊分析

一些定理及其证明

首先我们来定义一些名词：

border：若 $k$ 满足 $s[1\cdots k]=s[n-k+1\cdots n]$ ，则称 $s[1\cdots k]$ 为 $s$ 的 border。

period：若 $k$ 满足 $s[1\cdots n-k]=s[k+1\cdots n]$ ，那么 $k$ 是 $s$ 的一个周期。

不难发现，如果 $s$ 有一个长为 $k$ 的 border，那么就会有一个长为 $n-k$ 的 period。

WPL

WPL，即弱周期引理。

它的内容是：若 $p,q$ 均为 $s$ 的 period，且 $p+q\leq|s|$ ，则 $\gcd(p,q)$ 为 $s$ 的周期。

证明

由裴蜀定理，我们知道 $ap+bq=\gcd(p,q)$ 的解一定存在。

考虑模拟裴蜀定理证明的过程，钦定 $p\leq q$ ，那么有边界条件 $p=1$ ，此时该引理必然成立。

对于 $1<p\leq q$ 的情况，假设我们已经完成了 $(x,y)$ 的证明，其中 $x<p\or y<q$ 。由于 $p+q\leq|s|$ ，那么一定有 $k\in[1,|s|]$ ， $k\leq |s|-q$ 和 $k>p$ 其中一者已经被证明，手推一下不难发现上面两种情况可以推出 $q-p$ 是 $s$ 的周期，通过辗转相除可得 $\gcd(p,q)$ 为 $s$ 的周期。

PL

PL，即周期引理。

其内容为：若 $p,q$ 均为 $s$ 的 period，且 $p+q-\gcd(p,q)\leq|s|$ ，则 $\gcd(p,q)$ 为 $s$ 的周期。

证明较为复杂。

神秘结论

证明见 cmd 的博客。

即 $s$ 的长度达到 $n/2$ 的 border 长度构成一个等差数列，且将一个串的所有 border 按长度排序后，可以被划分成 $O(\log n)$ 个等差数列。

例题

P5287 JOJO

首先将询问离线成一个操作树。

考虑对一个二元组 $(c,len)$ 进行完全匹配的 KMP，考虑贡献。每次对查找到对于新串的匹配长度进行贡献统计即可。

但是，KMP 是均摊的，也就是说，在操作树上无法保证复杂度。

那么考虑对于一个周期，直接跳除周期外的剩余长度即可，注意这次比较是给跳一次 $nxt$ 的串做的。这和上面所证明的 被划分成 O(log n) 个等差数列 相符。

时间复杂度上界 $O(n\log n)$ 。

// Problem: P5287 [HNOI2019] JOJO
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5287
// Memory Limit: 500 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-25 19:05:48
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod=998244353;
struct str{
	int l,r,c;
}s[1000001];
int nxt[1000001];
int geta(int x,int y){//st:x ed:y
	return (x+y)*(y-x+1)/2;
}
vector<int> v[1000001];
int ans[1000001];
int nw;
int getnxt(int x){
	if(x==0)return -1;
	if(s[nxt[x]].r>s[x].r/2){
		int per=x-nxt[x];
		return nxt[x]%per+per;
	}
	else return nxt[x];
}
int insert(int c,int len){
	if(len==0)return 0;
	nw++;
	s[nw]={s[nw-1].r+1,s[nw-1].r+1+len-1,c};
	if(nw==1)return geta(1,len-1);
	int p=getnxt(nw-1),atl=nxt[nw-1],mp=0,res=0;
	while(p!=-1){
		// if(nw==16&&len==764&&c=='p')cerr<<p<<" "<<nxt[p]<<"\n";
		// cerr<<nw<<" "<<p<<" "<<atl<<"\n";
		int pp=0;
		if(c==s[p+1].c)pp=s[p+1].r-s[p+1].l+1;
		if(min(pp,len)>mp){
			res+=geta(mp+1+s[atl].r,min(pp,len)+s[atl].r);
			mp=min(pp,len);
		}
		if(pp==len){
			nxt[nw]=atl+1;
			break;
		}
		atl=nxt[p];
		p=getnxt(p);
	}
	if(s[1].c==c&&mp<len){
		res+=(len-mp)*(s[1].r-s[1].l+1);
		nxt[nw]=1;
	}
	return res;
}
struct line{
	int to,link,len,c;
}E[2000001];
int head[1000005],tot;
int pcnt=1,qtop[1000005];
void addE(int u,int v,int x,int c){
	E[++tot].to=v;
	E[tot].link=head[u];
	E[tot].len=x;
	E[tot].c=c;
	head[u]=tot;
	return;
}
// int C=0;
void dfs(int now,int f,int len,int c,int nowans){
	int nww=nw;
	nowans+=insert(c,len);
	int nww2=nw;
	// if(C%100==0)cerr<<C<<"\n";
	// C++;
	// cerr<<(char)c<<" "<<len<<" "<<nxt[nw]<<"\n";
	for(auto p:v[now])ans[p]=nowans;
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==f)continue;
		dfs(E[i].to,now,E[i].len,E[i].c,nowans);
	}
	nw=nww;
	if(nww2!=nww)nxt[nww2]=0;
	return;
}
signed main(){
	ios::sync_with_stdio(0);
	int nowpcnt=1;
	char cc;
	int op,ll;
	int q;
	cin>>q;
	qtop[0]=1;
	for(int i=1;i<=q;i++){
		cin>>op>>ll;
		if(op==1){
			cin>>cc;
			qtop[i]=++pcnt;
			v[pcnt].push_back(i);
			addE(nowpcnt,pcnt,ll,(int)cc);
			nowpcnt=pcnt;
		}else{
			qtop[i]=qtop[ll];
			v[qtop[i]].push_back(i);
			nowpcnt=qtop[i];
		}
	}
	dfs(1,0,0,0,0);
	for(int i=1;i<=q;i++)cout<<ans[i]%mod<<"\n";
	return 0;
}

细节较多，比如跳等差数列时要跳到 $nxt[x]\bmod (x-nxt[x])+(x-nxt[x])$ （先跳到等差数列末，再跳到下一个等差数列）等。

P3546

均摊分析题。

不难发现，对于循环相同的两个串 $S_1$ 和 $S_2$ ，如果把 $S_1$ 和 $S_2$ 拼起来，一定能满足 $A$ 串为新串的 border。

同样的，在 $S$ 上取出的前缀是不相交的，那么 $B$ 串就一定是去除 $A$ border 后剩余串的最长 border。设该值为 $t_i$ ，其中 $i$ 为 $A$ 长度，那么题目就是让我们求 $\max(len_A+t_{lenA})$ 。

考虑预处理 $t_i$ 。首先我们可以知道有 $t_i+2\geq t_{i-1}$ 。因为这个 border 每次掐头缩尾的变换（ $t_{i-1}-2\leq t_i$ ）。考虑均摊。我们有 $t_{\frac{n}{2}}=0$ ，而每次的值最多上升 $2$ ，最多上升 $n$ 次，最坏情况也只会移动 $O(n)$ 次。所以每次先暴力 $t_{i-1}\leftarrow t_i+2$ ，然后逐次递减找到最大值即可。

字符串匹配使用哈希即可。

// Problem: P3546 [POI2012] PRE-Prefixuffix
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3546
// Memory Limit: 64 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-26 08:33:31
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
char s[1000001];
const int base=277,mod=998244353;
long long hsh[1000001],_[1000001]={1};
long long gethsh(int l,int r){
	return ((hsh[r]-hsh[l-1]*_[r-l+1]%mod)+mod)%mod;
}
int t[1000001],n;
int pi[1000001];
int main(){
	ios::sync_with_stdio(0);
	for(int i=1;i<=1000000;i++)_[i]=_[i-1]*base%mod;
	cin>>n;
	cin>>(s+1);
	for(int i=1;i<=n;i++)hsh[i]=(hsh[i-1]*base+s[i])%mod;
	for(int i=n/2-1;i>=0;i--){
		t[i]=min(t[i+1]+2,n/2-i);
		for(;t[i]>0;t[i]--)if(gethsh(i+1,i+t[i])==gethsh(n-i-t[i]+1,n-i))break;
	}
	for(int i=2;i<=n;i++){
		int j=pi[i-1];
		while(j>0&&s[i]!=s[j+1])j=pi[j];
		if(s[i]==s[j+1])j++;
		pi[i]=j;
	}
	int now=n;
	int ans=0;
	do{
		now=pi[now];
		if(now<n/2)ans=max(ans,now+t[now]);
	}while(now!=0);
	cout<<ans;
	return 0;
}

Manacher

Manacher 通常用于处理最长回文子串。你说得对，但是这东西哈希也能在相同的时间复杂度做。你说得对，但是 Manacher 给我们提供了更多的信息。

先来讲 hash 做法，具体就是因为答案一定是 $O(n)$ 的，所以我们每次进行暴力遍历，如果发现该回文中心可以做到比原来的答案大，那么可以直接从此处暴力遍历并逐一增加答案。不难发现时间复杂度为 $O(n)$ 的。

这样做有一点点小问题，就是不能真正处理出以每个可以成为回文中心的点的最长回文半径（需要 $O(n\log n)$ ，即二分），而 Manacher 很好的解决了这个问题。

定义 $d_1$ 为回文串长度为奇数时一个回文中心的最长回文半径，如串 $abcbga$ ， $d_1[3]=2$ 。

定义 $d_2$ 为回文串长度为偶数时一个回文中心的最长回文半径，如串 $bddfsa$ ， $d_2[2]=1$ 。

思想

定义一个操作叫做回文翻转，即通过之前的信息进行转移（类似于 Z 函数）。考虑我们记录下目前所有回文中心的最长回文串中右端点最靠右的位置，如果当前位置被该回文串包含，那么就有 $\min(r-pos+1,s[l+r-pos])\to s[pos]$ 的转移，然后再进行暴力扩增。时间复杂度均摊 $O(n)$ 。

注意计算时可以加入一些字符来处理偶回文串和边界。

板子题

直接使用上面的思路即可。

// Problem: P3805 【模板】manacher
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3805
// Memory Limit: 512 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-26 10:36:19
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int p[22000005];
char s[22000005],c;
int main(){
	ios::sync_with_stdio(0);
	int pos=0;
	s[++pos]='*';
	s[++pos]='#';
	while((c=cin.get())&&c!=-1){
		// cerr<<(int)c<<"\n";
		if(c!=' '&&c!='\n'&&c!='\r')s[++pos]=c,s[++pos]='#';
	}
	s[++pos]='^';
	int n=pos;
	int l=1,r=1,ans=0;
	p[1]=1;
	for(int i=2;i<=n;i++){
		if(i<=r)p[i]=min(p[l+r-i],r-i+1);
		else p[i]=1;
		while(s[i-p[i]]==s[i+p[i]])p[i]++;
		if(i&1)ans=max(ans,(p[i]-1)/2*2+1);
		else ans=max(ans,p[i]/2*2);
		if(i+p[i]-1>r)l=i-p[i]+1,r=i+p[i]-1;
	}
	cout<<ans;
	return 0;
}

PPT 里没有 manacher 的练习题，我就先自己找一些题了。

题：P1659，P1723，*P4987，*P3501，**P4287，**P4555，*P5446（md hash 都能过），*P6216，P9606，**CF17E。

下面就不放代码了。

*P4987

统计答案是 trival 的，即对于当前回文中心最长回文串的长度大于 $l$ 则答案加一。

考虑断环为链，由于最长回文半径不会大于 $\frac{n}{2}$ ，所以向左右拓宽 $\frac{n}{2}$ 个字符即可（这个拓宽与回文中心是否显式有一定关系，如果保证该回文串必须有显式的回文中心，那么拓宽 $\frac{n-1}{2}$ 个字符就行了）。其实直接拼 $3$ 个原串也是可以的，懒一点可以写后面这个，但是在某些题中写后面这个要特判回文串大于 $n$ 的情况。

第一次写题就不要那么懒了。

这道题的回文串必须有显式的回文中心，谢谢你不让我的 Manacher 多插入 $O(n)$ 个字符。

*P3501

参见一篇题解的做法（虽然我的不太一样）：

考虑对于每个字母在这次 Manacher 时认为相等的字符存下来，如 $to['0']='1',to['1']='0',to['\#']='\#'$ 。这样在 Manacher 时可以直接比对 $s[i-p[i]]$ 和 $to[s[i+p[i]]]$ 。

注意这道题中的 Manacher 不太一样，所以需要严格计算，即去掉边界，然后只算不显式的回文中心。

**P4287

典中典之在 Manacher 过程中统计答案。

考虑直接在 Manacher 枚举回文串中检验当前非显式回文中心的回文串的左半部分是否为一个非显式回文中心的回文串即可（可以使用之前求出来的信息 $O(1)$ 检验）。

// Problem: P4287 [SHOI2011] 双倍回文
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4287
// Memory Limit: 500 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-26 16:16:10
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int n,pos,ans;
char op,s[1000005];
int p[1000005];
void rnans(int i){
	if(i%2==0&&p[i]>1&&p[i]/2%2==0&&p[i-p[i]/2]>p[i]/2)ans=max(ans,p[i]/2*2);
	return;
}
int main(){
	ios::sync_with_stdio(0);
	cin>>n;
	s[++pos]='*';
	s[++pos]='#';
	for(int i=1;i<=n;i++){
		cin>>op;
		s[++pos]=op;
		s[++pos]='#';
	}
	s[++pos]='^';
	n=pos;
	p[1]=1;
	int l=1,r=1;
	for(int i=2;i<=n-1;i++){
		if(i<=r)p[i]=min(r-i+1,p[l+r-i]);
		else p[i]=1;
		rnans(i);
		while(s[i-p[i]]==s[i+p[i]])p[i]++,rnans(i);
		if(i+p[i]-1>r)l=i-p[i]+1,r=i+p[i]-1;
	}
	cout<<ans;
	return 0;
}

**P4555

Manacher 好题。

Manacher 不止可以处理出什么最长回文子串和每个点的最长回文半径，还能处理出以该点为左或右端点所延伸出的最长回文串。

这道题本可以 Manacher + 线段树解决，不难想，但是实现起来较为复杂，特判点较多，大致就是维护目前这个点作为右端点是最小的回文中心。

但是我们可以利用类似差分的方法解决。考虑每次找到最大回文子串后可以只对这个回文串的左右区间端点处的值取 $\max$ ，然后最后正着和倒着都扫一遍，如对于右端点延伸出来的最长回文串，一定有 $r_{i-1}\leftarrow\max(r_{i-1},r_i-2)$ 。稍微感性理解一下，有点像动态规划一样的思路，不难发现在保证 $r_i$ 已经最优的情况下一定最优。

那么这道题就是求 $r_i+l_{i+1}$ 的最大值了。总时间复杂度 $O(n)$ 。

// Problem: P4555 [国家集训队] 最长双回文串
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4555
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-26 19:24:30
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int pl[1000005],pr[1000005],p[2000001];
char s[2000005],tp[2000005];
int n,pos;
int main(){
	ios::sync_with_stdio(0);
	cin>>(tp+1);
	n=strlen(tp+1);
	int org=n;
	for(int i=1;i<=org;i++)pl[i]=pr[i]=1;
	s[++pos]='*';
	s[++pos]='#';
	for(int i=1;i<=n;i++){
		s[++pos]=tp[i];
		s[++pos]='#';
	}
	s[++pos]='^';
	n=pos;
	int l=1,r=1,nowp=0;
	p[1]=1;
	for(int i=2;i<=n-1;i++){
		if(s[i]>='a'&&s[i]<='z')nowp++;
		if(i<=r)p[i]=min(r-i+1,p[l+r-i]);
		else p[i]=1;
		while(s[i-p[i]]==s[i+p[i]])p[i]++;
		int len,lpos,rpos;
		if(i&1)len=(p[i]-1)/2*2+1,lpos=nowp-len/2,rpos=nowp+len/2;
		else len=p[i]/2*2,lpos=nowp-len/2+1,rpos=nowp+len/2;
		pr[rpos]=max(pr[rpos],len);
		pl[lpos]=max(pl[lpos],len);
		if(i+p[i]-1>r)l=i-p[i]+1,r=i+p[i]-1;
	}
	for(int i=1;i<=org;i++)pl[i]=max(pl[i],pl[i-1]-2);
	for(int i=org;i>=1;i--)pr[i]=max(pr[i],pr[i+1]-2);
	int ans=2;
	for(int i=1;i<org;i++){
		ans=max(ans,pr[i]+pl[i+1]);
	}
	cout<<ans;
	return 0;
}

*P5446

这题我觉得用 Manacher 真的过了，hash 就行了。

hash 的做法就是倒序枚举长度，如果翻转后的长度大于等于原串长度，那么直接判断剩下的串是不是长度为奇数的回文串，如果小于那么就判断该前缀翻转后是不是还是原串前缀，如果是就能从翻转后的长度转移过来，上面的操作通过 hash 都能 $O(1)$ 解决。

Manacher 的做法类似。同样的倒序枚举和分讨，只不过预处理出来了回文串的长度罢了。

*P6216

一堆东西的大杂烩。

对于 区间查询出现次数，考虑我们只关注右端点，那么这个问题可以用 区间查询其在原串出现时的右端点位置个数，该信息可差分，所以可以 KMP 出来跑两次前缀和。

对于每个最长回文半径，先预处理出能产生贡献的右端点位置，然后使用二阶前缀和处理询问即可，处理时细节较多。

草，正常马拉车统计答案好像只用 p[i]-1，小丑了。

**CF17E

这题我想了两个做法，结果全假了，所以只能看题解。

这里就有一个很套路但是就是想不到的转化：考虑相交回文串不好求，所以就求不相交回文串就行了。

后面就简单了。考虑记录 $f_i$ 为左端点为 $i$ 的回文子串个数， $g_i$ 为右端点为 $i$ 的回文子串个数，那么对于一个回文子串 $[l,r]$ ，与他不相交的回文子串个数为 $\sum_{i=1}^{l-1}g_i+\sum_{i=r+1}^{n}f_i$ 。使用差分计算 $g_i$ 和 $f_i$ ，然后再前缀和跑一遍把询问转成 $O(1)$ 求，再求一次二阶前缀和，把每个回文中心的询问一起处理了，时间复杂度 $O(n)$ 。

最后除以 $2$ 要乘上其逆元 $25561994$ 。

还卡前缀和的空间，唉。

// Problem: Palisection
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF17E
// Memory Limit: 125 MB
// Time Limit: 2000 ms
// Start coding at 2023-12-27 09:57:50
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod=51123987;
int n,pos,org;
bool aa;
char tp[2000005];
char s[4000005];
int p[4000005];
int f[2000005],g[2000005];
// int pref1[2000005],preg1[2000005];
int pref2[2000005],preg2[2000005];
bool bb;
int qug(int l,int r){
	if(l<=0)l=1;
	// if(r>org)r=org+1;
	if(r<l)return 0;
	return ((preg2[r]%mod-preg2[l-1]%mod)+mod)%mod;
}
int quf(int l,int r){
	if(l<=0)l=1;
	// if(r>org)r=org+1;
	if(r<l)return 0;
	return ((r-l+1)*f[org]%mod-(pref2[r-1]-pref2[l-2])%mod+mod)%mod;
}
long long tot;
signed main(){
	ios::sync_with_stdio(0);
	cin>>n;
	cin>>(tp+1);
	s[++pos]='*';
	s[++pos]='#';
	for(int i=1;i<=n;i++){
		s[++pos]=tp[i];
		s[++pos]='#';
	}
	s[++pos]='^';
	org=n;
	n=pos;
	int l=1,r=1,nowp=0,lpos,rpos;
	p[1]=p[2]=p[n-1]=p[n-2]=1;
	for(int i=3;i<=n-2;i++){
		if(s[i]>='a'&&s[i]<='z')nowp++;
		if(i<=r)p[i]=min(r-i+1,p[l+r-i]);
		else p[i]=1;
		while(s[i-p[i]]==s[i+p[i]])p[i]++;
		int len=p[i]-1;
		tot+=(len+1)/2;
		if(i&1){
			lpos=nowp-len/2;
			rpos=nowp+len/2;
			f[lpos]++,f[nowp+1]--;
			g[rpos+1]--,g[nowp]++;
		}else{
			lpos=nowp-len/2+1;
			rpos=nowp+len/2;
			f[lpos]++,f[nowp+1]--;
			g[rpos+1]--,g[nowp+1]++;
		}
		if(i+p[i]-1>r)l=i-p[i]+1,r=i+p[i]-1;
	}
	tot%=mod;
	// cerr<<tot<<"\n";
	long long ans=tot*(tot-1)%mod;
	for(int i=1;i<=org;i++)f[i]+=f[i-1],g[i]+=g[i-1];//,cerr<<f[i]<<" "<<g[i]<<"\n";
	// for(int i=1;i<=org;i++)pref1[i]=pref1[i-1]+f[i],preg1[i]=preg1[i-1]+g[i];
	// for(int i=1;i<=org;i++)pref2[i]=pref2[i-1]+pref1[i],preg2[i]=preg2[i-1]+preg1[i];
	for(int i=1;i<=org;i++)f[i]=f[i-1]+f[i],g[i]=g[i-1]+g[i],f[i]%=mod,g[i]%=mod;
	for(int i=1;i<=org;i++)pref2[i]=pref2[i-1]+f[i],preg2[i]=preg2[i-1]+g[i],pref2[i]%=mod,preg2[i]%=mod;
	nowp=0;
	for(int i=3;i<=n-2;i++){
		if(s[i]>='a'&&s[i]<='z')nowp++;
		int len=p[i]-1;
		if(i&1){
			lpos=nowp-len/2;
			rpos=nowp+len/2;
			ans-=qug(lpos-1,nowp-1)+quf(nowp+1,rpos+1);
			ans=(ans+mod)%mod;
		}else{
			lpos=nowp-len/2+1;
			rpos=nowp+len/2;
			ans-=qug(lpos-1,nowp-1)+quf(nowp+2,rpos+1);
			ans=(ans+mod)%mod;
		}
	}
	cout<<ans*25561994%mod;
	return 0;
}

Trie

原理就不提了，直接上一些应用。

较为板子

题：P2580，SP4033。

Trie+DP

题：**UVA1401。

**UVA1401

这道 dp 很显然，不过 hash 更好做，因为 hash 可以支持 $f[i]\to \cdots$ 和 $\cdots\to f[i]$ 两种转移方式，而 Trie 只能支持前一种，后一种的复杂度则是假的。

首先考虑 dp，选择 $f[i]\to \cdots$ 的转移方式，就有类似于 $f[i]=\sum f[j]$ 的转移方程式。这个转移的子串是互为前缀的，而 Trie 的建立就是依托于前缀。于是就可以在长串上直接遍历 Trie 来判断转移即可。

当然也可以将字符串翻转做后缀 Trie，但是这个不如直接使用前缀 Trie，因为它也有相同的局限性。

注意多测清空的正确性与完备性。

// Problem: Remember the Word
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/UVA1401
// Memory Limit: 0 MB
// Time Limit: 3000 ms
// Start coding at 2023-12-27 16:23:18
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int t[400002][27],tcnt=1;
bool exi[400002];
const int mod=20071027;
void insert(string &s){
	int siz=s.size();
	int now=1;
	for(int i=0;i<siz;i++){
		if(!t[now][s[i]-'a'])t[now][s[i]-'a']=++tcnt;
		now=t[now][s[i]-'a'];
	}
	exi[now]=1;
	return;
}
void clear(int now){
	for(int i=0;i<=26;i++){
		if(t[now][i])clear(t[now][i]);
		t[now][i]=0;
	}
	exi[now]=0;
	return;
}
string p,s;
int n,dp[300005],mlen,C;
int main(){
	ios::sync_with_stdio(0);
	while(cin>>p){
		clear(1);
		s.clear();
		tcnt=1;
		mlen=0;
		cin>>n;
		for(int i=1;i<=n;i++){
			cin>>s;
			mlen=max(mlen,(int)s.size());
			insert(s);
		}
		int psiz=p.size();
		dp[0]=1;
		for(int i=0;i<psiz;i++){
			int len=min(mlen,psiz-i);
			int now=1;
			for(int j=i;j<=i+len-1;j++){
				now=t[now][p[j]-'a'];
				if(!now)break;
				if(exi[now])dp[j+1]=(dp[j+1]+dp[i])%mod;
			}
		}
		C++;
		cout<<"Case "<<C<<": "<<dp[psiz]<<"\n";
		for(int i=0;i<=psiz;i++)dp[i]=0;
	}
	return 0;
}

Trie 上计数

题：UVA11732（注意最后加哨兵字符）。

一些题思维量较少，所以就不写了。

杂题

题：*P7469

*P7469

首先利用 Trie 的思想，发现其实串的贡献只与每个位置开始的字符串对于第一个串的匹配长度有关。而不难发现当匹配位数相同时，匹配到的位置下标越小越好，所以可以直接贪心匹配。

写完之后 WA 了，发现还要去重。

可以使用 Trie，但是被卡空间了，用 unordered_map 顶天到 90pts TLE，于是只能用 hash 暴力匹配了。

hash 匹配可以记录下之前答案的哈希值，答案最多有 $\frac{n^2}{2}+n$ 个，所以根本不慌爆空间。

然后离散化就行了，时间复杂度 $O(n^2\log n)$ ，有更优解法，但是基本都是要带几个常数的。

而且 Trie 可以链式前向星建边，不过这样就需要遍历一遍已有的边，时间复杂度 $O(n|\Sigma|)$ ，空间复杂度 $O(n)$ 。

90pts 代码：

// Problem: P7469 [NOI Online 2021 提高组] 积木小赛
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P7469
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-27 20:22:10
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
char s[3001],p[3001];
unordered_map<int,int> t[26];
int tcnt=1,tmp,ans;
bool vis[4500002];
void insert(const int &l,const int &r){
	int now=1;
	for(int i=l;i<=r;i++){
		tmp=t[p[i]-'a'][now];
		if(!tmp){
			t[p[i]-'a'][now]=++tcnt;
			tmp=tcnt;
		}
		now=tmp;
		ans+=vis[now]^1;
		if(!vis[now])vis[now]=1;
	}
	return;
}
int n;
int ssiz,psiz;
int main(){
	ios::sync_with_stdio(0);
	cin>>n;
	cin>>s>>p;
	ssiz=strlen(s);
	psiz=strlen(p);
	for(int i=0;i<psiz;i++){
		int nowp=i;
		for(int j=0;j<ssiz;j++){
			if(p[nowp]==s[j]&&nowp<psiz)nowp++;
		}
		insert(i,nowp-1);
	}
	cout<<ans;
	return 0;
}

100pts 做法（hash）：

md 数组开小了调试了半天。

// Problem: P7469 [NOI Online 2021 提高组] 积木小赛
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P7469
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-27 20:22:10
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
char s[3001],p[3001];
long long t[5000001];
int tcnt;
const long long mod=2005091020050911,base=51971;
long long hsh=0;
int n;
int ssiz,psiz,ans;
int main(){
	ios::sync_with_stdio(0);
	cin>>n;
	cin>>s>>p;
	ssiz=strlen(s);
	psiz=strlen(p);
	for(int i=0;i<psiz;i++){
		int nowp=i;
		hsh=0;
		for(int j=0;j<ssiz;j++){
			if(p[nowp]==s[j]&&nowp<psiz){
				t[++tcnt]=(hsh=(hsh*base+(s[j]-'a'+1))%mod);
				nowp++;
			}
		}
	}
	sort(t+1,t+tcnt+1);
	ans=unique(t+1,t+tcnt+1)-t-1;
	cout<<ans;
	return 0;
}

AC 自动机

思想和 KMP 差不多，用于处理多模式串匹配。

思想

之前写 KMP 的时候，我画了一张 KMP 在字符串上运作的图，这里其实就是把这个图搬到了树上。

首先建出 Trie，考虑建出树上的 fail 指针。

对于第一层，我们发现它们的 fail 都是根结点。

对于后面几层，回顾我们之前 KMP 的思想，假定我们已经算出这个节点以上所有层所有节点的 fail，又该怎么做。

首先，最重要的是，理解 fail 的本质，它的本质就是多模式串的 border，border 即从根到节点形成的串的后缀与 Trie 上插入过的串的前缀相同的。我们要求的就是当 border 最长时，Trie上插入过的串的前缀 的节点位置。

所以，考虑我们已经求出了节点 $u$ 及其小于等于其深度的其他节点的 fail：

首先，我们调用 $u$ 的 fail，找到 $rt\to u$ 路径上最长 border。

这个时候利用动态规划的思想，不难发现这个时候是最优情况，那么就只需要看这个节点有没有 $v$ 对于 $u$ 对应的儿子即可。如果有，那么直接把 $v$ 的 fail 指向这个儿子，没有的话，就又要找到一个次长的 border 再次尝试拓宽一个字符，而不难发现，红色节点的 fail 指向的节点所代表的前缀一定是红色节点的其中一个后缀，也是黄色节点的其中一个后缀，所以我们又得到了第 $k$ 长 border 的最长 border 是第 $k+1$ 长的 border 这个结论。那么我们只需要像 KMP 一样跳 fail 就行了。

建立 fail 指针时注意特判根结点就行了。

对于查询，每次匹配到没有该字符的儿子时就跳 fail，如果跳到根结点都没有能够匹配的就跳过当前字符，当遍历到带有字符串结尾标记的字符就答案 +1。

但是实际操作中，上面的 跳 fail 操作需要较多判断，并且带有结尾标记的字符的 fail 如果指向了另一个带有结尾标记的字符就会统计漏。考虑在建立 fail 指针的时候把 跳 fail 的过程简化。

考虑如果遍历到一个不存在的节点，我们完全可以把这个节点直接指向其父亲（必须是存在的点）的 fail 的对应儿子。这样的话需要把 $0$ 的所有儿子都指向根结点，但是查询的步骤大大减少。

如果是求出现了多少模板串，那么可以直接跳 fail 统计。如果跳到一个已经统计过的节点就不用继续统计下去了。然后每次直接跳儿子即可。

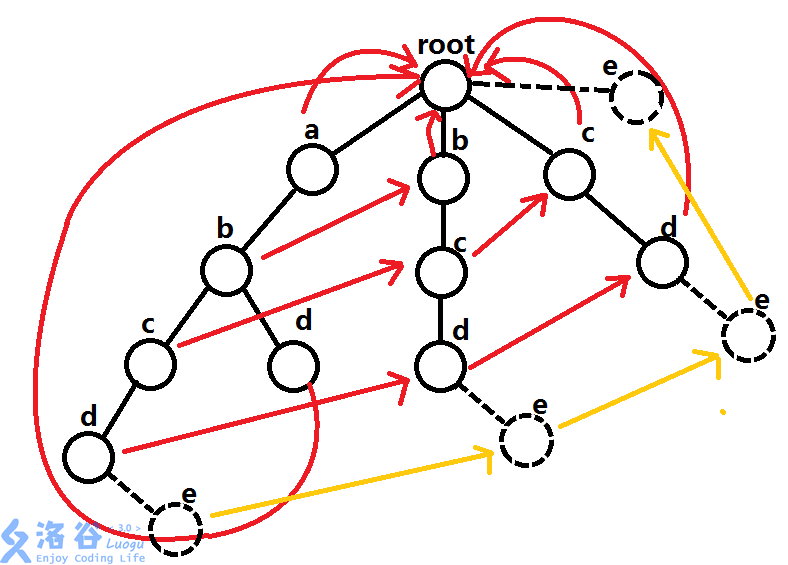
…解释一下上面说的 把这个节点直接指向其父亲（必须是存在的点）的 fail 的对应儿子 为什么能减少查询的步骤。考虑我们是 BFS 一棵 Trie 的，所以我们连接的顺序是倒序赋值的，所以遇到这种情况时：

（图是褐的）

对于字符 e，你会发现其实所有的虚点都赋为了 $0$ ，而加入连接 $rt$ 的 e 是存在的话，我们会发现其他虚点都被赋成了那个存在的 e 的位置，这样就不用一个 fail 一个 fail 的跳了。

这题板子有点多啊…

板子题

P3808 简单版

直接照上面的思路做就行了。

// Problem: P3808 【模板】AC 自动机（简单版）
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3808
// Memory Limit: 512 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-28 10:45:26
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int t[1000005][26],tcnt=1;
int cnt[1000005],fail[1000005];
void insert(string &s){
	int siz=s.size();
	int now=1;
	for(int i=0;i<siz;i++){
		if(!t[now][s[i]-'a'])t[now][s[i]-'a']=++tcnt;
		now=t[now][s[i]-'a'];
	}
	cnt[now]++;
	return;
}
queue<int> q;
void getfail(){
	for(int i=0;i<=25;i++)t[0][i]=1,fail[t[1][i]]=1;
	q.push(1);
	while(!q.empty()){
		int u=q.front();
		q.pop();
		for(int i=0;i<=25;i++){
			if(t[u][i]){
				int k=fail[u];
				while(k>0&&!t[k][i])k=fail[k];
				fail[t[u][i]]=t[k][i];
				q.push(t[u][i]);
			}else t[u][i]=t[fail[u]][i];
		}
	}
	return;
}
int calc(string &p){
	int siz=p.size();
	int res=0,now=1;
	for(int i=0;i<siz;i++){
		now=t[now][p[i]-'a'];
		int tmp=now;
		while(tmp>1&&cnt[tmp]!=-1){
			res+=cnt[tmp];
			cnt[tmp]=-1;
			tmp=fail[tmp];
		}
	}
	return res;
}
string s,p;
int n;
int main(){
	ios::sync_with_stdio(0);
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>s;
		insert(s);
	}
	getfail();
	cin>>p;
	cout<<calc(p);
	return 0;
}

数据太水了，代码实现可能有误。

P3796 加强版

首先 $O(t|T||S|)$ 是 trival 的。

AC 自动机上每次暴力跳 fail 统计答案，每个节点存一个 vector<int> 记录信息（其实不用，因为模式串两两不同）。最后遍历一边所有模式串即可。这里没有像简单版一样的均摊，所以复杂度是 $O(|T||S|)$ 的。

这道题由于 $|S|$ 很小，所以可以通过。

代码：

// Problem: P3796 【模板】AC 自动机（加强版）
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3796
// Memory Limit: 128 MB
// Time Limit: 3000 ms
// Start coding at 2023-12-28 14:41:34
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int t[10502][26],tcnt=1,fail[10502];
vector<int> v[10502],buc[151];
int cnt[151];
void insert(string &s,const int &id){
	int siz=s.size();
	int now=1;
	for(int i=0;i<siz;i++){
		if(!t[now][s[i]-'a'])t[now][s[i]-'a']=++tcnt;
		now=t[now][s[i]-'a'];
	}
	v[now].push_back(id);
	return;
}
queue<int> q;
void getfail(){
	for(int i=0;i<26;i++)t[0][i]=1,fail[t[1][i]]=1;
	q.push(1);
	while(!q.empty()){
		int u=q.front();
		q.pop();
		for(int i=0;i<26;i++){
			if(t[u][i]){
				int k=fail[u];
				while(k&&!t[k][i])k=fail[k];
				fail[t[u][i]]=t[k][i];
				q.push(t[u][i]);
			}else t[u][i]=t[fail[u]][i];
		}
	}
	return;
}
void clear(){
	for(int i=1;i<=tcnt;i++){
		for(int j=0;j<26;j++){
			t[i][j]=0;
		}
		fail[i]=0;
		v[i].clear();
	}
	tcnt=1;
	for(int i=1;i<=150;i++)cnt[i]=0,buc[i].clear();
	return;
}
void calc(string &p){
	int siz=p.size();
	int now=1,tmp;
	for(int i=0;i<siz;i++){
		now=t[now][p[i]-'a'];
		tmp=now;
		while(tmp>1){
			for(auto k:v[tmp])cnt[k]++;
			tmp=fail[tmp];
		}
	}
	return;
}
string s[151],p;
int n,maxc;
int main(){
	ios::sync_with_stdio(0);
	while(cin>>n&&n){
		for(int i=1;i<=n;i++){
			cin>>s[i];
			insert(s[i],i);
		}
		getfail();
		cin>>p;
		calc(p);
		maxc=0;
		for(int i=1;i<=n;i++){
			buc[cnt[i]].push_back(i);
			maxc=max(maxc,cnt[i]);
		}
		cout<<maxc<<"\n";
		for(auto k:buc[maxc])cout<<s[k]<<"\n";
		clear();
	}
	return 0;
}

考虑优化。

考虑我们 fail 指针整体来看的一个形态。因为每个点都有出边（ $1$ 除外），而对于所有前缀，有 border 的话会连向其他节点，而如果没有，就一定是连向 $1$ 的。所以 fail 指针一定形成一棵树，而我们统计答案就是统计一个点到根路径上所有点的贡献加一，使用树上差分即可。时间复杂度降至 $O(t(|T|+\sum|S|))$ 。

注意其实不需要初始化第一层的 fail，如果树上差分这种方式就会建出来一堆重边影响统计。

// Problem: P3796 【模板】AC 自动机（加强版）
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3796
// Memory Limit: 128 MB
// Time Limit: 3000 ms
// Start coding at 2023-12-28 15:44:12
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
struct line{
	int link,to;
}E[30005];
int tot,head[10503],w[10503];
int t[10502][26],tcnt=1;
int org[10502],fail[10502],cnt[151];
void insert(string &s,const int &id){
	int siz=s.size();
	int now=1;
	for(int i=0;i<siz;i++){
		if(!t[now][s[i]-'a'])t[now][s[i]-'a']=++tcnt;
		now=t[now][s[i]-'a'];
	}
	org[now]=id;
	return;
}
queue<int> q;
void addE(int u,int v){
	E[++tot].link=head[u];
	E[tot].to=v;
	head[u]=tot;
	return;
}
void addfail(int u,int v){
	addE(u,v);
	addE(v,u);
	fail[u]=v;
	return;
}
void getfail(){
	for(int i=0;i<26;i++)t[0][i]=1;
	q.push(1);
	while(!q.empty()){
		int u=q.front();
		q.pop();
		for(int i=0;i<26;i++){
			if(t[u][i]){
				int k=fail[u];
				while(k&&!t[k][i])k=fail[k];
				addfail(t[u][i],t[k][i]);
				q.push(t[u][i]);
			}else t[u][i]=t[fail[u]][i];
		}
	}
	return;
}
void clear(){
	for(int i=0;i<=tcnt;i++){
		org[i]=0;
		fail[i]=0;
		head[i]=w[i]=0;
		for(int j=0;j<26;j++)t[i][j]=0;
	}
	tcnt=1,tot=0;
	for(int i=1;i<=150;i++)cnt[i]=0;
	return;
}
void calc(string &p){
	int siz=p.size();
	int now=1;
	for(int i=0;i<siz;i++){
		now=t[now][p[i]-'a'];
		w[now]++;
	}
	return;
}
void dfs(int now,int f){
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==f)continue;
		dfs(E[i].to,now);
		w[now]+=w[E[i].to];
	}
	if(org[now])cnt[org[now]]=w[now];
	return;
}
int n;
string s[151],p;
int main(){
	ios::sync_with_stdio(0);
	while(cin>>n&&n){
		for(int i=1;i<=n;i++){
			cin>>s[i];
			insert(s[i],i);
		}
		getfail();
		cin>>p;
		calc(p);
		dfs(1,0);
		int maxc=0;
		for(int i=1;i<=n;i++)maxc=max(maxc,cnt[i]);
		cout<<maxc<<"\n";
		for(int i=1;i<=n;i++)if(cnt[i]==maxc)cout<<s[i]<<"\n";
		clear();
	}
	return 0;
}

P5357 二次加强版

不用判重，开 $2\times10^5$ 个 vector 记录编号即可。使用加强版优化后的思路，时间复杂度 $O(|S|+\sum|T|)$ 。

// Problem: P5357 【模板】AC 自动机（二次加强版）
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5357
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-28 19:34:14
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
struct line{
	int to,link;
}E[600006];
int head[300005],tot;
void addE(int u,int v){
	E[++tot].link=head[u];
	E[tot].to=v;
	head[u]=tot;
	return;
}
int t[200005][26],tcnt=1;
int fail[200005],cnt[200005];
vector<int> v[200005];
int w[200005];
void addfail(int u,int v){
	addE(u,v);
	addE(v,u);
	fail[u]=v;
	return;
}
void insert(string &s,const int &id){
	int siz=s.size();
	int now=1;
	for(int i=0;i<siz;i++){
		if(!t[now][s[i]-'a'])t[now][s[i]-'a']=++tcnt;
		now=t[now][s[i]-'a'];
	}
	v[now].push_back(id);
	return;
}
queue<int> q;
void getfail(){
	for(int i=0;i<26;i++)t[0][i]=1;
	q.push(1);
	while(!q.empty()){
		int u=q.front();
		q.pop();
		for(int i=0;i<26;i++){
			if(t[u][i]){
				int k=fail[u];
				while(k&&!t[k][i])k=fail[k];
				addfail(t[u][i],t[k][i]);
				q.push(t[u][i]);
			}else t[u][i]=t[fail[u]][i];
		}
	}
	return;
}
void calc(string &p){
	int siz=p.size();
	int now=1;
	for(int i=0;i<siz;i++){
		now=t[now][p[i]-'a'];
		w[now]++;
	}
	return;
}
void dfs(int now,int f){
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==f)continue;
		dfs(E[i].to,now);
		w[now]+=w[E[i].to];
	}
	for(auto o:v[now])cnt[o]=w[now];
	return;
}
int n;
string s[200001],p;
int main(){
	ios::sync_with_stdio(0);
	cin>>n;
	for(int i=1;i<=n;i++)cin>>s[i],insert(s[i],i);
	getfail();
	cin>>p;
	calc(p);
	dfs(1,0);
	for(int i=1;i<=n;i++)cout<<cnt[i]<<"\n";
	return 0;
}

例题

题：*P3966，**P3121，**P3041，*P4052，*P4045，**P2444，UVA1127，**P2414，**P2292，***P2336。

*P3966

不难发现就是板子题。沿用 Manacher 算法处理边界的思路，在每个单词之间插入一个 {（z 的 ASCII 值加一所对应的字母），然后跑一遍差分优化型多模式串匹配即可。

**P3121

建立 AC 自动机，记录结尾标识即其长度并且下放 fail 树上的标识，每次遍历到结尾标识就直接回退状态 + 栈弹出即可。

实际上的栈使用 vector 实现。

// Problem: P3121 [USACO15FEB] Censoring G
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3121
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-29 09:23:37
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int t[100002][26],tcnt=1;
int fail[100002],len[100002];
int vers[100002];
vector<char> st;
struct line{
	int to,link;
}E[200002];
int head[100002],tot;
void addE(int u,int v){
	E[++tot].link=head[u];
	E[tot].to=v;
	head[u]=tot;
	return;
}
void addfail(int u,int v){
	addE(u,v);
	addE(v,u);
	fail[u]=v;
}
void dfs(int now,int f){
	if(!len[now])len[now]=len[f];
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==f)continue;
		dfs(E[i].to,now);
	}
	return;
}
void insert(string &s){
	int siz=s.size();
	int now=1;
	for(int i=0;i<siz;i++){
		if(!t[now][s[i]-'a'])t[now][s[i]-'a']=++tcnt;
		now=t[now][s[i]-'a'];
	}
	len[now]=siz;
	return;
}
queue<int> q;
void getfail(){
	for(int i=0;i<26;i++)t[0][i]=1;
	q.push(1);
	while(!q.empty()){
		int u=q.front();
		q.pop();
		for(int i=0;i<26;i++){
			if(t[u][i]){
				int k=fail[u];
				while(k&&!t[k][i])k=fail[k];
				addfail(t[u][i],t[k][i]);
				q.push(t[u][i]);
			}else t[u][i]=t[fail[u]][i];
		}
	}
	return;
}
void work(string &p){
	int siz=p.size();
	int now=1,vcnt=0;
	vers[0]=1;
	for(int i=0;i<siz;i++){
		st.push_back(p[i]);
		now=t[now][p[i]-'a'];
		vers[++vcnt]=now;
		if(len[now]){
			for(int j=1;j<=len[now];j++){
				st.pop_back();
				vcnt--;
			}
			now=vers[vcnt];
		}
	}
	return;
}
string s,p;
int n;
int main(){
	ios::sync_with_stdio(0);
	cin>>p>>n;
	for(int i=1;i<=n;i++)cin>>s,insert(s);
	getfail();
	dfs(1,0);
	work(p);
	for(auto o:st)cout<<o;
	return 0;
}

**P3041

ACAM + dp。

考虑建立状态 $dp_{i,j}$ 为长度为 $i$ ，目前到了状态 $j$ 的最大组合技个数。那么显然有转移：

dp_{i,son_{j,T}}=\max (dp_{i,son_{j,T}},dp_{i,j}+cnt_{son{j,T}})(T\in\{'A','B','C'\})

$cnt$ 数组用 fail 树下放的方式预处理。 $dp$ 数组预处理为 $-\infty$ ， $dp_{0,1}=0$ 。

// Problem: P3041 [USACO12JAN] Video Game G
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3041
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-29 09:51:15
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int t[303][3],tcnt=1;
int cnt[303],fail[303];
void insert(string &s){
	int siz=s.size();
	int now=1;
	for(int i=0;i<siz;i++){
		if(!t[now][s[i]-'A'])t[now][s[i]-'A']=++tcnt;
		now=t[now][s[i]-'A'];
	}
	cnt[now]++;
	return;
}
struct line{
	int link,to;
}E[10001];
int head[303],tot;
void addE(int u,int v){
	E[++tot].link=head[u];
	E[tot].to=v;
	head[u]=tot;
	return;
}
void addfail(int u,int v){
	addE(u,v);
	addE(v,u);
	fail[u]=v;
	return;
}
queue<int> q;
void getfail(){
	for(int i=0;i<3;i++)t[0][i]=1;
	q.push(1);
	while(!q.empty()){
		int u=q.front();
		q.pop();
		for(int i=0;i<3;i++){
			if(t[u][i]){
				int k=fail[u];
				while(k&&!t[k][i])k=fail[k];
				addfail(t[u][i],t[k][i]);
				q.push(t[u][i]);
			}else t[u][i]=t[fail[u]][i];
		}
	}
}
void dfs(int now,int f){
	cnt[now]+=cnt[f];
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==f)continue;
		dfs(E[i].to,now);
	}
	return;
}
int n,k;
string s;
int dp[1001][303];
int main(){
	ios::sync_with_stdio(0);
	cin>>n>>k;
	for(int i=1;i<=n;i++)cin>>s,insert(s);
	getfail();
	dfs(1,0);
	for(int i=0;i<=k;i++)for(int j=0;j<=tcnt;j++)dp[i][j]=-1e9;
	dp[0][1]=0;
	for(int i=1;i<=k;i++){
		for(int j=0;j<=tcnt;j++){
			for(int k=0;k<3;k++){
				dp[i][t[j][k]]=max(dp[i][t[j][k]],dp[i-1][j]+cnt[t[j][k]]);
			}
		}
	}
	int maxx=0;
	for(int i=0;i<=tcnt;i++)maxx=max(maxx,dp[k][i]);
	cout<<maxx;
	return 0;
}

*P4052

考虑我们为了转移时能过连续转移（即长度 $i-1\to i$ 转移），利用补集思想把求可读文本数量转化为不可读文本数量。总文本数量则易求，为 $26^m$ 。

那么在下放 fail 树上标记后，显然有以下转移：

dp_{i,son_{j,T}}=\sum dp_{i-1,j}(end[son_{j,T}]=0,T\in \{'A',\cdots,'Z'\})

暴力转移即可。

ACAM 的 dp 状态大多数是一样的。

*P4045

考虑 $N\leq10$ ，想到状压。设计状态 $dp_{i,j,s}$ 代表目前拼了 $i$ 个字符，在 Trie 上第 $j$ 个节点，拼的字符串集合为 $s$ 。不难想到有 $dp_{i,son_{j,T},s}=\sum dp_{i-1,j,s}(end_{son_{j,T}}=0)$ 。对于 $s$ 的转移差不多相同。

对于输出方案，考虑先记忆化搜索搜出能转移到终点的节点，然后再顺着能转移的节点进行遍历即可。

这题有点抽象。

**P2444

好题，充分考察了对 ACAM 的理解程度。

考虑首先建出 ACAM，不难发现对于一个串来讲，直接走 ACAM 的一条边就是加一个字符在这个串后面，那么考虑如果能无限加字符到后面，那么就能无限走，也就是说删除结尾节点之后能遍历到的点有环。那么 Tarjan 找环即可。

注意自环的判断，这里使用了较为偷懒的方法判环，就规避了自环。

// Problem: P2444 [POI2000] 病毒
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2444
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-30 10:21:12
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int t[30002][2],tcnt=1;
int fail[30002];
bool ed[30002];
void insert(string &s){
	int siz=s.size();
	int now=1;
	for(int i=0;i<siz;i++){
		if(!t[now][s[i]-'0'])t[now][s[i]-'0']=++tcnt;
		now=t[now][s[i]-'0'];
	}
	ed[now]=1;
	return;
}
struct line{
	int to,link;
}E[200001];
int head[100001],tot;
void addE(int u,int v){
	E[++tot].link=head[u];
	E[tot].to=v;
	head[u]=tot;
	return;
}
void addfail(int u,int v){
	addE(u,v);
	addE(v,u);
	fail[u]=v;
	return;
}
void dfs(int now,int f){
	ed[now]|=ed[f];
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==f)continue;
		dfs(E[i].to,now);
	}
	return;
}
queue<int> q;
void getfail(){
	for(int i=0;i<2;i++)t[0][i]=1;
	q.push(1);
	while(!q.empty()){
		int u=q.front();
		q.pop();
		for(int i=0;i<2;i++){
			if(t[u][i]){
				int k=fail[u];
				while(k&&!t[k][i])k=fail[k];
				addfail(t[u][i],t[k][i]);
				q.push(t[u][i]);
			}else t[u][i]=t[fail[u]][i];
		}
	}
	return;
}
stack<int> st;
int dfn[30002],low[30002],inst[30002],dfncnt;
void tarjan(int now){
	st.push(now);
	inst[now]=1;
	dfn[now]=low[now]=++dfncnt;
	for(int i=0;i<2;i++){
		if(ed[t[now][i]])continue;
		if(dfn[t[now][i]]==0){
			tarjan(t[now][i]);
			low[now]=min(low[now],low[t[now][i]]);
		}
		else if(inst[t[now][i]])cout<<"TAK",exit(0);
	}
	if(low[now]==dfn[now]){
		if(st.top()==now)st.pop(),inst[now]=0;
	}
	return;
}
int n;
string s;
int main(){
	ios::sync_with_stdio(0);
	cin>>n;
	for(int i=1;i<=n;i++)cin>>s,insert(s);
	getfail();
	dfs(1,0);
	tarjan(1);
	cout<<"NIE";
	return 0;
}

**P2414

非常好的一道题。

首先考虑如果把所有串整下来串总长最大会达到 $10^{10}$ ，于是考虑在输入时就遍历 Trie，记录存在的（遍历到的）边，对于回退操作就直接暴力记录之前的状态和位置即可。这样建立 ACAM 的复杂度就降到了 $O(n)$ 。

然后考虑一个询问时如何处理。不难发现其实就是在 Trie 上根到所询问节点路径上所有节点在对应的 fail 树上进行该点到根的路径加一，最后单点查。链加单点查可以转化为单点加子树查，那么可以使用 dfn 序 + 树状数组进行维护。

这样就只剩下最后一个问题了，如何快速维护不同点的查询？首先离线询问，考虑不难发现 Trie 树上对于单个串前缀的所有状态只有 $10^5$ 个，而上面却要查询 $O(n^2)$ 次，不难发现可以通过有用状态之间的转移进行优化，那么就是 dfs 一遍 Trie 树，进入一个节点时单点修改该位置的元素，出该节点时单点修改删除该位置元素的贡献即可。到达一个字符串结尾时，正常处理询问，注意区分什么时候在 Trie 上跑，什么时候在 fail 树上跑。

// Problem: P2414 [NOI2011] 阿狸的打字机
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2414
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-30 16:51:06
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
struct line{
	int to,link;
}E[200001];
int head[100001],tot;
void addE(int u,int v){
	E[++tot].link=head[u];
	E[tot].to=v;
	head[u]=tot;
	return;
}
int t[100002][26],tcnt=1;
bool rl[100002][26];
int fail[100002],idw[100002];
vector<pair<int,int> > v[100002];
string tp;
int vernw[100002],ans[100002],idcnt;
void addfail(int u,int v){
	addE(u,v);
	addE(v,u);
	fail[u]=v;
	return;
}
queue<int> q;
void getfail(){
	for(int i=0;i<26;i++)t[0][i]=1;
	q.push(1);
	while(!q.empty()){
		int u=q.front();
		q.pop();
		for(int i=0;i<26;i++){
			if(t[u][i]){
				int k=fail[u];
				while(k&&!t[k][i])k=fail[k];
				addfail(t[u][i],t[k][i]);
				q.push(t[u][i]);
			}else t[u][i]=t[fail[u]][i];
		}
	}
	return;
}
int L[100002],R[100002],rk[100002],dfncnt;
void dfs(int now,int f){
	L[now]=++dfncnt;
	rk[dfncnt]=now;
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==f)continue;
		dfs(E[i].to,now);
	}
	R[now]=dfncnt;
	return;
}
int m,x,y;
int tr[100002];
int lowbit(int x){
	return x&-x;
}
void mdf(int x,int v){
	while(x<=dfncnt){
		tr[x]+=v;
		x+=lowbit(x);
	}
	return;
}
int qu(int x){
	int res=0;
	while(x>0){
		res+=tr[x];
		x-=lowbit(x);
	}
	return res;
}
void getans(int now,int f){
	mdf(L[now],1);
	for(auto o:v[now])ans[o.first]=qu(R[o.second])-qu(L[o.second]-1);
	for(int i=0;i<26;i++)if(rl[now][i])getans(t[now][i],now);
	mdf(L[now],-1);
	return;
}
int main(){
	ios::sync_with_stdio(0);
	cin>>tp;
	int tpz=tp.size(),nw=1,nver=0;
	vernw[0]=1;
	for(int i=0;i<tpz;i++){
		if(tp[i]>='a'&&tp[i]<='z'){
			if(!t[nw][tp[i]-'a']){
				rl[nw][tp[i]-'a']=1;
				t[nw][tp[i]-'a']=++tcnt;
			}
			nw=t[nw][tp[i]-'a'];
			vernw[++nver]=nw;
		}else if(tp[i]=='P'){
			idw[++idcnt]=nw;
		}else if(nver>=1)nw=vernw[--nver];
	}
	getfail();
	dfs(1,0);
	cin>>m;
	for(int i=1;i<=m;i++){
		cin>>x>>y;
		v[idw[y]].push_back(make_pair(i,idw[x]));
	}
	getans(1,0);
	for(int i=1;i<=m;i++)cout<<ans[i]<<"\n";
	return 0;
}

**P2292

极好的一道状压优化 dp 状态的题。

首先不难想到 $O(m|S||T|)$ 或者 $O(mn|T|)$ 的暴力转移思路，即在原串上按长度暴力转移能到达的地方，可以用 hash $O(n)$ 转移，也可用 Trie $O(|S|)$ 转移，但是他们复杂度均不优秀。

考虑优化，看到 $|S|\leq 20$ ，不难想到状压长度，建出 ACAM，定义 $msg_{u,l}$ 表示在节点 $u$ 处能否从当前字符之前 $l$ 个字符转移过来。这是一个 bool，所以可以压到一个 int 里。那么考虑转移时就要记录一个 $dp_{i,l}$ 表示当前串长度为 $i$ ，并且第 $i-l$ 个字符前的字符串合法，这同样可以状压到一个 int 里，那么只需要记录 $dp_i\and msg_u$ 为不为 $0$ 即可。每次 $dp_{i+1}\leftarrow ((dp_i\times2)\and (2^{20}-1)+ans_i)$ 转移即可。

注意 fail 树上下放计算 $msg$ 数组。 $dp$ 数组则有初始值 $dp_0=2^{20}-1$ 。

// Problem: P2292 [HNOI2004] L 语言
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2292
// Memory Limit: 128 MB
// Time Limit: 1000 ms
// Start coding at 2023-12-30 20:00:46
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
struct line{
	int to,link;
}E[4000006];
int head[2000002],tot;
void addE(int u,int v){
	E[++tot].link=head[u];
	E[tot].to=v;
	head[u]=tot;
	return;
}
int t[2000005][26],tcnt=1;
int fail[2000005],msg[2000005];
void addfail(int u,int v){
	addE(u,v);
	addE(v,u);
	fail[u]=v;
	return;
}
void insert(string &s){
	int siz=s.size();
	int now=1;
	for(int i=0;i<siz;i++){
		if(!t[now][s[i]-'a'])t[now][s[i]-'a']=++tcnt;
		now=t[now][s[i]-'a'];
	}
	msg[now]|=(1<<(siz-1));
	return;
}
queue<int> q;
void getfail(){
	for(int i=0;i<26;i++)t[0][i]=1;
	q.push(1);
	while(!q.empty()){
		int u=q.front();
		q.pop();
		for(int i=0;i<26;i++){
			if(t[u][i]){
				int k=fail[u];
				while(k&&!t[k][i])k=fail[k];
				addfail(t[u][i],t[k][i]);
				q.push(t[u][i]);
			}else t[u][i]=t[fail[u]][i];
		}
	}
	return;
}
void dfs(int now,int f){
	msg[now]|=msg[f];
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==f)continue;
		dfs(E[i].to,now);
	}
	return;
}
const int oo=(1<<20)-1;
bool dp[2000005];
int maxp;
int pre20[2000005];
int calc(string &p){
	maxp=0;
	int siz=p.size();
	int now=1;
	pre20[0]=oo;
	for(int i=0;i<siz;i++){
		now=t[now][p[i]-'a'];
		dp[i]=((pre20[i]&msg[now])!=0);
		pre20[i+1]=((pre20[i]<<1)&oo)+dp[i];
		if(dp[i])maxp=i+1;
	}
	return maxp;
}
int n,m;
string s;
int main(){
	ios::sync_with_stdio(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>s;
		insert(s);
	}
	getfail();
	dfs(1,0);
	for(int i=1;i<=m;i++){
		cin>>s;
		cout<<calc(s)<<"\n";
	}
	return 0;
}

***P2336

这题实在太好了，看起来像一个很不起眼的字符串匹配裸题，但是却包含了非常多的思想。

首先我们发现建 AC 自动机的复杂度是 $O(n|\Sigma|)$ ，已经爆了，但是我们先不管如何优化，考虑如何统计答案。

首先来翻译问题：第一问是求一个模式串能由多少个文本串匹配，第二问是求一个文本串能匹配多少个模式串。我们将模式串的 AC 自动机建出来。

考虑正常暴力做法，第二问可以直接 $O(|T|+\sum|S|)$ 匹配，然后贡献回退时间复杂度为 $O(\sum|S|)$ ，总复杂度爆炸。

既然暴力不行，那么我们按顺序来，考虑第一问怎么做。我们显然发现每个后缀可能会有不同串匹配上，那么如果下传 fail 树上标记的 id 或暴力跳 fail 统计的最坏时间复杂度均为 $O(n^2)$ ，无法通过。考虑优化。我们沿用阿狸的打字机一题的思路，对于我们走到的每一个前缀进行 fail 树上的操作，但是由于此题需要求贡献并而不是贡献和，所以需要一些 Trick 来除去多余贡献。

不难发现第一问就是 fail 树上到根链修改单点查询，转化为单点修改子树查，可以用树状数组维护。具体就是对于每个文本串暴力在 AC 自动机上跳，每个串跳到的所有点进行到根路径 +1 的操作，并将这一个串的所有贡献做并。然后最后询问每个模式串结尾节点得到答案。

这里使用一个 Trick：先对 AC 自动机上访问到的节点按 fail 树的 dfs 序排序，然后减去贡献就是相邻两个点的 $LCA$ 到根的链上所有点 -1。很好证明，考虑原本不加贡献直接离线下来用 dfs 序排序，然后每次令这次询问的点与上次询问的点的 $LCA$ 到这次询问的点的路径 +1，手玩一下发现这种做法是对的，然后其实这种做法和上面那种做法是一样的。

那么对于第一问，我们的思路就清晰了，对每个串先遍历一遍得到其 dfs 序，排序过后树状数组维护单点修改子树查询，最后对于每一个模板串进行查询贡献和。

模仿第一问，我们第二问的思路同样有了：同样是先遍历一遍得到其 dfs 序，然后在模式串的结尾先单点修改，然后对于每一个前缀进行到根链查询，可以转化为子树修改单点查。然后每次暴力进行每个前缀的查询，同样使用上面那个 Trick 减去多余的贡献，回退的话需要使用原来的 dfs 序全部做反操作。

然后最大的问题来了：建 AC 自动机的时间复杂度都爆炸了，你说怎么办呢？

考虑对每一个点都开一个动态开点线段树来存储 这个点的 x 指针在 Trie 上指向哪里，在 节点复制 那一步中利用可持久化的思想将两棵线段树合并在一起，具体就是同时遍历两棵线段树，如果此时该子树不存在，那么就直接将这个链接指向该子树，如果到了叶子，那么就可以直接把 fail 指向之前的那棵子树，查询时正常单点查询自己的后继即可。

代码看起来非常难写，呜呜…

upd：第一问是可以离线树上差分做的，但是第二问不行。

// Problem: P2336 [SCOI2012] 喵星球上的点名
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2336
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Start coding at 2024-01-02 09:13:48
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+5,maxm=1e4+5;
int xds[maxn<<5],ch[maxn<<5][2];
int rt[maxn],rtcnt;
void addl(int l,int r,int q,int ts,int &id){
	if(!id)id=++rtcnt;
	if(l==r)return xds[id]=ts,void();
	int mid=(l+r)/2;
	if(q<=mid)addl(l,mid,q,ts,ch[id][0]);
	else addl(mid+1,r,q,ts,ch[id][1]);
	return;
}
int ask(int l,int r,int q,int id){
	if(!id)return 0;
	if(l==r)return xds[id];
	int mid=(l+r)/2;
	if(q<=mid)return ask(l,mid,q,ch[id][0]);
	else return ask(mid+1,r,q,ch[id][1]);
}
queue<int> q;
int tcnt=1;
int fail[maxn],num[maxn];
struct line{
	int to,link;
}E[maxn<<2];
int head[maxn],tot;
void addE(int u,int v){
	E[++tot].link=head[u];
	E[tot].to=v;
	head[u]=tot;
	return;
}
void addfail(int u,int v){
	addE(u,v);
	addE(v,u);
	fail[u]=v;
	return;
}
void merge(int l,int r,int u,int &v){
	if(!v)return v=u,void();
	if(l==r){
		addfail(xds[v],xds[u]);
		q.push(xds[v]);
		return;
	}
	int mid=(l+r)/2;
	merge(l,mid,ch[u][0],ch[v][0]);
	merge(mid+1,r,ch[u][1],ch[v][1]);
	return;
}
int insert(const int &siz,int *s){
	int now=1;
	for(int i=1;i<=siz;i++){
		if(!ask(0,maxm,s[i],rt[now]))addl(0,maxm,s[i],++tcnt,rt[now]);
		now=ask(0,maxm,s[i],rt[now]);
		// cerr<<now<<" "<<s[i]<<" "<<s[1]<<" "<<i<<"\n";
	}
	return now;
}
void getfail(){
	xds[0]=1;
	q.push(1);
	while(!q.empty()){
		int u=q.front();
		q.pop();
		merge(0,maxm,rt[fail[u]],rt[u]);
	}
	return;
}
int L[maxn],rk[maxn],R[maxn],dfncnt;
void dfs(int now,int f){
	L[now]=++dfncnt;
	rk[dfncnt]=now;
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==f)continue;
		dfs(E[i].to,now);
	}
	R[now]=dfncnt;
	return;
}
int dep[maxn],siz[maxn],fa[maxn],hson[maxn];
void dfs1(int now,int f){
	siz[now]=1;
	fa[now]=f;
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==f)continue;
		dep[E[i].to]=dep[now]+1;
		dfs1(E[i].to,now);
		siz[now]+=siz[E[i].to];
		if(siz[E[i].to]>siz[hson[now]])hson[now]=E[i].to;
	}
	return;
}
int ltop[maxn];
void dfs2(int now,int top){
	ltop[now]=top;
	if(!hson[now])return;
	dfs2(hson[now],top);
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==fa[now]||E[i].to==hson[now])continue;
		dfs2(E[i].to,E[i].to);
	}
	return;
}
int LCA(int u,int v){
	while(ltop[u]!=ltop[v]){
		if(dep[ltop[u]]>dep[ltop[v]])u=fa[ltop[u]];
		else v=fa[ltop[v]];
	}
	return (dep[u]>dep[v]?v:u);
}
vector<int> resv;
void getdfn(const int &siz,int *s){
	int now=1;
	resv.clear();
	for(int i=1;i<=siz;i++){
		// cerr<<now<<" ";
		now=ask(0,maxm,s[i],rt[now]);
		if(now==0)now=1;
		resv.push_back(L[now]);
	}
	return;
}
int tr1[maxn],tr2[maxn];
int lowbit(int x){
	return x&-x;
}
void mdf(int x,int v,int *tr){
	while(x<=100000){
		tr[x]+=v;
		x+=lowbit(x);
	}
	return;
}
int qsum(int x,int *tr){
	int res=0;
	while(x>0){
		res+=tr[x];
		x-=lowbit(x);
	}
	return res;
}
vector<int> v[50005];
int temp[100005],ans1[maxn],ans2[maxn],ed[maxn];
int len,n,m,tp;
int main(){
	ios::sync_with_stdio(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>len;
		for(int j=1;j<=len;j++){
			cin>>tp;
			v[i].push_back(tp);
		}
		v[i].push_back(10001);
		cin>>len;
		for(int j=1;j<=len;j++){
			cin>>tp;
			v[i].push_back(tp);
		}
	}
	for(int i=1;i<=m;i++){
		cin>>len;
		for(int j=1;j<=len;j++)cin>>temp[j];
		ed[i]=insert(len,temp);
	}
	getfail();
	dfs(1,0);
	dfs1(1,0);
	dfs2(1,1);
	for(int i=1;i<=m;i++){
		mdf(L[ed[i]],1,tr2);
		mdf(R[ed[i]]+1,-1,tr2);
	}
	for(int i=1;i<=n;i++){
		int si=v[i].size();
		for(int j=1;j<=si;j++){
			temp[j]=v[i][j-1];
		}
		getdfn(si,temp);
		sort(resv.begin(),resv.end());
		int lst=1;
		for(auto ap:resv)ans2[i]+=qsum(ap,tr2)-qsum(L[LCA(rk[ap],rk[lst])],tr2),lst=ap;
		lst=1;
		for(auto ap:resv)mdf(ap,1,tr1),mdf(L[LCA(rk[lst],rk[ap])],-1,tr1),lst=ap;
	}
	for(int i=1;i<=m;i++){
		ans1[i]=qsum(R[ed[i]],tr1)-qsum(L[ed[i]]-1,tr1);
		cout<<ans1[i]<<"\n";
	}
	for(int i=1;i<=n;i++)cout<<ans2[i]<<" ";
	return 0;
}

还剩余一些 CF 上的 ACAM 题未做，之后再补。

子序列自动机

用来处理子序列问题，不太常用。

思想

考虑维护一个 $nxt_{i,c}$ 指在第 $i$ 个位置之后字符 $c$ 第一次出现的位置。这样可以让此时转移到 $i$ 状态时能够选择到下一个最近的位置，不难发现这样一定最优。

构建方式

字符集较小

当字符集较小时，我们可以倒序记录目前该位置及其以后每个字符集中的元素距离当前位置的最近的一个的位置，倒序更新每个点的 $nxt$ 数组并更新字符集内部情况即可。

时空复杂度均为 $O(n|\Sigma|)$ 。询问复杂度 $O(|T|)$ 。

字符集较大

由于上面那种构建方式的时空复杂度均过大，考虑换一种思路。

我们用 vector 给每个字符集里的元素的出现位置开一个桶，初始将它排序，每次要查询时在某个桶里二分查找下一个位置即可。

构建复杂度为 $O(|\Sigma|\log n)$ ，空间复杂度 $O(n)$ ，询问复杂度 $O(|T|\log n)$ 。

板子题

直接套 字符集较大 时的做法即可。

// Problem: P5826 【模板】子序列自动机
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5826
// Memory Limit: 500 MB
// Time Limit: 2000 ms
// Start coding at 2024-01-02 17:12:09
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
vector<int> v[1000005];
int n,q,m;
void bulid(int *s){
	for(int i=1;i<=n;i++)v[s[i]].push_back(i);
	for(int i=1;i<=m;i++)v[i].push_back(n+1);
	return;
}
int query(int pos,int num){
	return *upper_bound(v[num].begin(),v[num].end(),pos);
}
int s[1000001],p[1000001],len;
int main(){
	ios::sync_with_stdio(0);
	cin>>n>>n>>q>>m;
	for(int i=1;i<=n;i++)cin>>s[i];
	bulid(s);
	for(int i=1;i<=q;i++){
		cin>>len;
		for(int j=1;j<=len;j++)cin>>p[j];
		int now=0;
		for(int j=1;j<=len;j++){
			now=query(now,p[j]);
			if(now==n+1){
				cout<<"No\n";
				break;
			}
		}
		if(now!=n+1)cout<<"Yes\n";
	}
	return 0;
}

例题

题：P3500，*P4608，*P4112（部分），**CF17C（其实不是序列自动机）。

*P4608

子序列自动机有一个几乎是板子的 dp 状态，就是 $dp_i$ 表示以 $i$ 开始的子序列的一些情况。

这道题基本相同，设 $dp_{i,j}$ 为 $X$ 串以 $i$ 开始， $Y$ 串以 $j$ 开始，有多少个公共子序列，显然有：

dp_{i,j}\leftarrow \sum_{c\in \Sigma}dp_{nxtX_{i,c},nxtY_{j,c}}+1

我们最终需要 $dp_{0,0}$ ，那么我们可以记忆化搜索。

至于为什么要加一，我们可以来分类讨论一下：

当 $X_i=Y_j$ 时，之后可能会有其他状态转移时需要这个位置的状态，而这种状态的转移对答案的贡献正好为 $1$ （多插入一个字符），符合我们对于以 $i$ 开始的定义。
另一种情况在记忆化搜索中不可能搜到。

对于输出方案，肯定有方案总字符数较少。

有一点点抽象。注意使用 $O(n|\Sigma|)$ 的建序列自动机的方式，这样不用 $O(\log n)$ 查找。

*P4112

非常典。

这道题的 $1,3$ 问要 SAM，这里暂不做探讨。

$a$ 的一个最短的子串，它不是 $b$ 的子序列。
$a$ 的一个最短的子序列，它不是 $b$ 的子序列。

第一问可以直接暴力从小到大枚举子串然后在 $b$ 中查找子序列。

第二问则需要 dp。

不难发现我们可以用 最后一个字符不同 的贪心策略，得到方程式：

f(i,null)=0,f(i,j)=\min_{nxt_{i,c}\not=null}f(nxt_{i,c},nxt_{j,c})+1

其中 $+1$ 在 $nxt_{j,c}=null$ 时代表的是最后我选 $c$ 字符一定使两者不同，在其他情况代表加入一个 $c$ 字符形成一个较优的子序列。 $f(i,j)$ 则代表两串分别在状态 $i,j$ 时还需要加多少个字符才能合法。

个人认为两串还需要交换一下 dp，这样似乎更加严谨。

下面这道题只是浅浅用了一些子序列自动机的思想，但是全是 dp，呜呜。

**CF17C

神仙 dp 题。

对于题中乱七八糟的操作，我们可以把它理解成在原串中选出一个子序列，然后把子序列复制几次。

那么我们可以暴力记录每个字母出现的次数，设 $to_{i,c}$ 为字母 $c$ 在 $i$ 及 $i$ 之后的第一次出现的位置，那么有：

f_{to_{i,'a'},a+1,b,c}=\sum f_{i,a,b,c}

b 与 c 的转移相同。

为什么直接转移到 $to_{i,p}$ 呢？分两种情况讨论：

当 $i=to_{i,p}$ 时，有 $s_i=p$ 。那么这里的 $a$ 可以无限复制，对应这里可以无限 $+1$ 。
当 $i\not=to_{i,p}$ 时，那么直接转移到后面后明显还可以继续无限复制，能达到要求。

故上面转移正确，虽然有点反直觉。

注意有初始值 $f_{1,0,0,0}=1$ 。当 $a+b+c=n$ 且 $\abs{a-b}\leq1\and\abs{b-c}\leq 1\and\abs{a-c}\leq1$ 时这个状态就可以加到总答案中。

至于为什么 $f_{0,0,0,0}$ 的初始值不能为 $1$ ，根据 $to$ 的奇妙定义，我们知道如果设置 $f_{0,0,0,0}$ 的话就会有 $f_{0,0,1,0}$ 类似的情况出现，具体类似于就是 $cnt_b=0$ 的情况。这样的无限加就会加多了。

杂题

目前还有 SA，SAM，PAM 等字符串结构还没有学习。

CF1080E

考虑 重排之后回文 的情况。很容易想到状压后 popcount 为 $0$ 或 $1$ ，但是这里要求每行每列都是回文的，所以暴力枚举子矩形左右端点，把 $26$ 位的各个出现次数映射到 hash，然后用 manacher 对 hash 后的值计算回文串个数。

对于出现次数不能构成回文串的串，我们可以把它的 hash 值设成 $-1,-2\cdots$ ，以保证不重复。