前言

从这里开始，信竞的路就开始向未来延伸了

之前觉得信息竞赛不过是打打电脑，敲敲代码，从来没想到这其实是对思维的一种锻炼。

信息竞赛的终端是NOI，也就是国赛，那场比赛会让一部分人极度高兴，也会让一部分人迷惘，无奈，最后退役，除这两者之外，也会有一些人陷入沉思——

无数高二的OIer，他们两年，三年，甚至五年，六年的OI生涯，就在走出NOI赛场的那一刻，彻底终结。

原文链接：link（经过2d左右的寻找终于找到了）

…

让我们开始吧…

什么是Splay？

用一个经典问题引入：

你需要维护一些数，其中需要提供以下操作：

  1. 插入 xx 数
  2. 删除 xx 数(若有多个相同的数，应只删除一个)
  3. 查询 xx 数的排名(排名定义为比当前数小的数的个数 +1+1 )
  4. 查询排名为 xx 的数
  5. 求 xx 的前驱(前驱定义为小于 xx，且最大的数)
  6. 求 xx 的后继(后继定义为大于 xx，且最小的数)

1≤n≤1051\leq n \leq 10^5

因为有操作2，这道题暴力的时间复杂度是 O(n2)O(n^2) 的。

那么，二叉搜索树就出现了——

二叉搜索树是一种二叉树的树形数据结构，其定义如下：

  1. 空树是二叉搜索树。
  2. 若二叉搜索树的左子树不为空，则其左子树上所有点的附加权值均小于其根节点的值。
  3. 若二叉搜索树的右子树不为空，则其右子树上所有点的附加权值均大于其根节点的值。
  4. 二叉搜索树的左右子树均为二叉搜索树。

上述定义来源于 OI Wiki。

二叉搜索树上的基本操作所花费的时间与这棵树的高度成正比。对于一个有 nn 个结点的二叉搜索树中，这些操作的最优时间复杂度为 O(log⁡n)O(\log n)，最坏为 O(n)O(n)。

而 Splay 的出现就是为了防止二叉搜索树退化成链从而导致不能保证时间复杂度。

如何实现Splay？

一些基本变量

rt tot fa[i] ch[i][0/1] v[i] cnt[i] stre_size[i]
根节点编号 节点个数 父亲 左右儿子编号 节点权值 权值出现次数 子树大小或其他

还有…

1
2
#define lson 0
#define rson 1

一些基本操作

maintain()

和 pushup() 是一个道理，更新子树大小或者题中要我们维护的信息。

1
2
3
4
5
6
void maintain(int x){
	stre_size[x]=stre_size[ch[x][rson]]+stre_size[ch[x][lson]]+cnt[x];//这个是维护子树大小
//	sum[x]=sum[ch[x][rson]]+sum[ch[x][rson]]+cnt[x]*v[x];//这个是维护权值和，但是多开一个数组
//还有其他各种各样的
    return;
}

get()

获取节点 xx 是父亲的哪个儿子。

1
2
3
bool get(int x){
    return ch[fa[x]][rson]==x;
}

clear()

用来销毁节点 xx。

1
2
3
4
void clear(int x){
    fa[x]=v[x]=cnt[x]=stre_size[x]=ch[x][lson]=ch[x][rson]=0;
    return;
}

旋转-rotate()

在讲 Splay 如何让二叉搜索树不退化成链前，先说说实现 Splay 最重要的操作：左旋与右旋。

没看明白？想想二叉搜索树的性质！旋转前后都要保证二叉搜索树的性质，也就是左 << 中 << 右！

假如说以上图右旋 2 节点为例，2 节点需要向上一层，根据二叉搜索树的性质，1 节点处的值是大于 2 节点处的值，那么在新树里，1 就是 2 的右儿子。同样的，可以推出 5 节点的值是大于 2 节点的值，同时 1 节点的值大于 5 节点的值，所以在新树中，5 是 1 的左儿子。

以此类推，我们可以推出旋转的通用方法：

  1. 假设要旋转的节点为 xx，它的父亲是 yy，xx 是 yy 的 chkchk 儿子（左 →0→ 0，右 →1→ 1），那么 xx 的 chkchk xorxor 11 儿子是 yy 的 chkchk 儿子，还要记得把这个儿子（如果这个儿子存在的话）的父亲设为 yy。
  2. yy 的父亲为 xx，xx 的 chkchk xorxor 11 儿子为 yy。（注意按顺序来）
  3. 设原来的 yy 的父亲是 zz，那么 xx 的父亲是 zz，如果 zz 存在（不为 00），那么设原来 zz 的 kk 儿子是 yy，现在 zz 的 kk 儿子是 xx。
  4. 最后从下到上更新信息即可。(易漏)
1
2
3
4
5
6
7
8
9
10
11
12
13
void rotate(int x){
    int y=fa[x],z=fa[y];
    bool chk=get(x);
    fa[y]=x;
    ch[y][chk]=ch[x][chk^1];
    if(ch[x][chk^1])fa[ch[x][chk^1]]=y;
    ch[x][chk^1]=y;
    fa[x]=z;
    if(z)ch[z][ch[z][rson]==y]=x;
    maintain(y);
    maintain(x);
    return;
}

splay()

Splay 的最核心操作，目的是把一个节点旋转到根节点上。

分为以下几种情况：

  1. zig操作：在 splay 操作开始时节点具有奇数深度时用于 splay 的最后一步。

直接将节点 xx 旋转即可。

甚至这个图和上面旋转的那个图一模一样…

  1. zig-zig操作：当节点的父亲与该节点都是他们的父亲的同侧儿子时使用。

可能有些抽象了。

如果还是直接旋转两次节点 xx 的话，这个图就会从这样

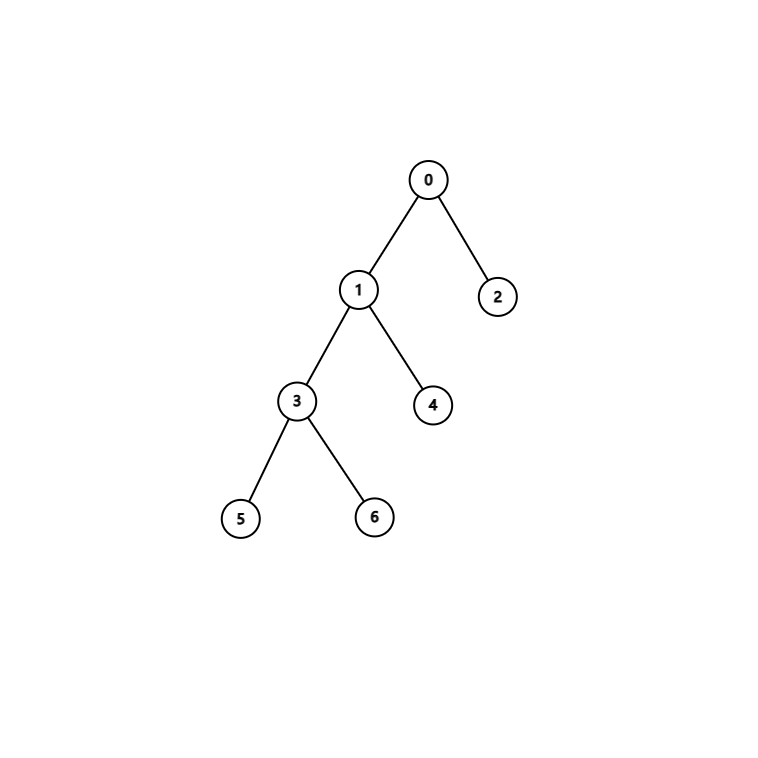
变成…

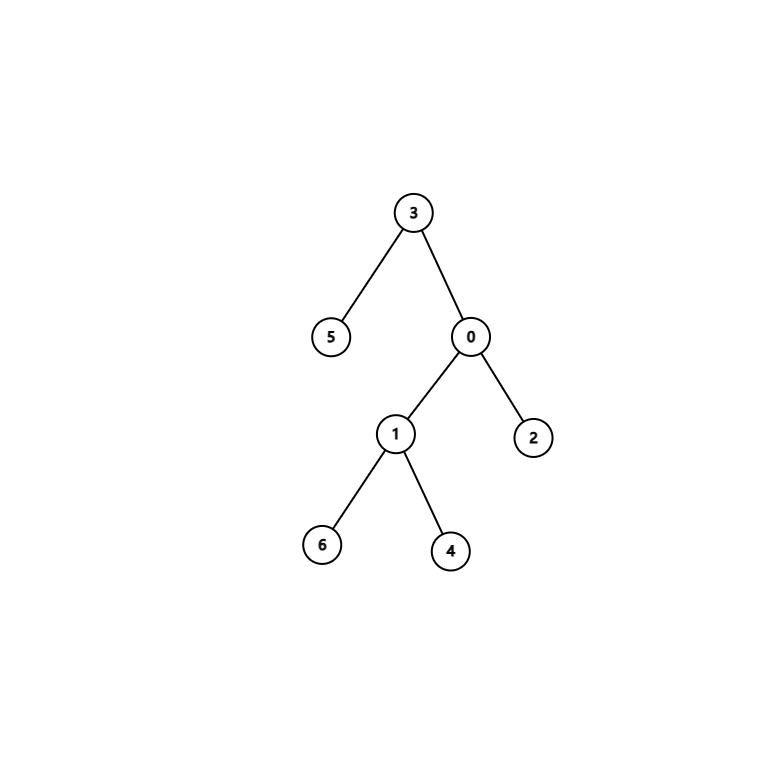
这样…

好像确实不是我们想要的，对吧？

稍微模拟一下过程可以发现，因为节点 00 无法旋转，那么应该先旋转节点 11，即待旋转节点 33 的父亲，在旋转节点 33。

具体过程演示：

整张图应该先变成这样：

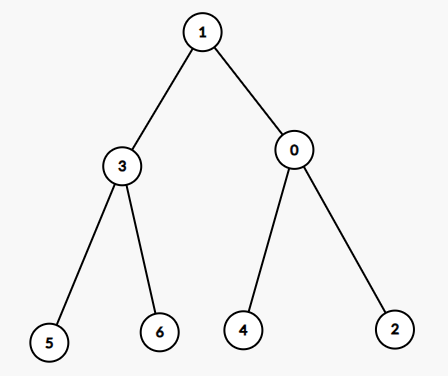
然后再旋转节点 33，变成这样：

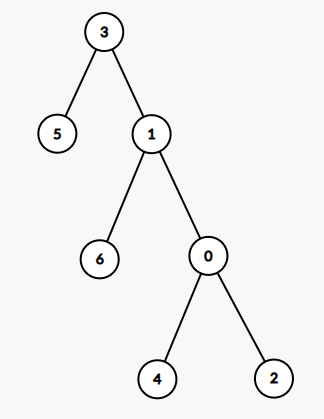
这就是我们想要的了，但是前提是节点 33 的爷爷节点 00 存在。

  1. zig-zag操作：当节点的父亲与该节点是他们的父亲的异侧儿子时使用。

还是老样子，先尝试只旋转节点 xx。

整张图的变换过程差不多长这样：

→→ →→

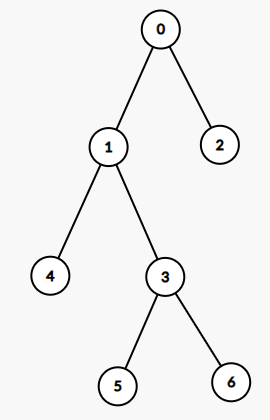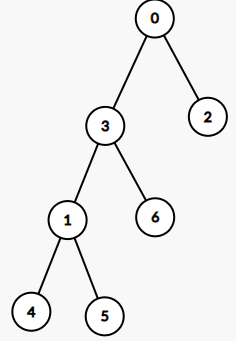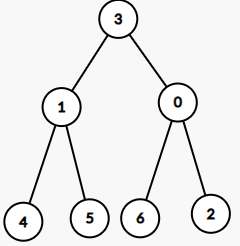
诶？这好像是就是我们需要的！

于是，针对于这种情况，旋转两次原来的节点 xx 即可。

整合上面三种情况，就可以写出 splay() 的代码了：

1
2
3
4
5
6
7
void splay(int x){
    for(;fa[x];rotate(x)){
        if(fa[fa[x]])rotate((get(x)==get(fa[x]))?fa[x]:x);
    }
    rt=x;
    return;
}

但是这可能不够，有些时候我们 splay 到一个特定节点就停了，所以还要新增一个参数，改进后的函数长这样：

1
2
3
4
5
6
7
void splay(int x,int tar=0){
    for(;fa[x]!=tar;rotate(x)){
        if(fa[fa[x]]!=tar)rotate(get(x)==get(fa[x])?fa[x]:x);
    }
    if(tar==0)rt=x;
    return;
}

insert()

插入分为这几步：

  1. 如果树是空的，直接插入根节点即可。
  2. 如果要插入的值与正遍历到的值相等，直接 cnt[cur]++ 即可。
  3. 如果要插入的值大于当前值，则向右遍历，小于则向左遍历，直到遍历到第一个空节点时插入。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
void insert(int x){
    if(!rt){
        v[++tot]=x;
        rt=tot;
        cnt[rt]++;
        maintain(rt);
        return;
    }
    int cur=rt,buf=fa[cur];
    while(1){
        if(v[cur]==x){
            cnt[cur]++;
            maintain(cur);
            maintain(buf);//爸爸也要上传信息!
            splay(cur);//最后都要splay!!!!!
            return;
        }
        buf=cur;
        cur=ch[cur][v[cur]<x];
        if(!cur){
            cnt[++tot]++;
            ch[buf][v[buf]<x]=tot;
            v[tot]=x;
            fa[tot]=buf;
            maintian(tot);
            maintain(buf);
            splay(tot);//最后都要splay!!!!!!!!!!!!!!!!!!
            return;
        }
    }
}

当然，如果是在特定的两个元素之间插入，那么可以将这两个元素先 splay 到根，此时这两个元素之间必然为空，直接插入即可。

1
2
3
4
5
6
7
8
9
10
11
void insert(int x,int l,int r){
    splay(l);
    splay(r,l);
    ch[r][lson]=++tot;
    v[tot]=x;
    cnt[tot]++;
    fa[tot]=r;
    maintain(tot);
    maintain(r);
    return;
}

（注：上面这种插入很少见，请谨慎使用）

即查询数 xx 的排名。

同样的，遍历一遍即可。

  1. 如果当前数的值大于 xx，则向左子树寻找。
  2. 如果当前数的值小于 xx，则将当前排名加上 stre_size[ch[cur][lson]]+cnt[cur] 在向右子树遍历。
  3. 当当前数正好等于 xx 或当前遍历到的节点为空时，返回当前排名 +1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int numx_rank_search(int x){
    int cur=rt,res=0;
    while(1){
        if(v[cur]>x){
            if(!ch[cur][lson]){
                splay(cur);
                return res+1;
            }
            cur=ch[cur][lson];
        }
        else{
            res+=stre_size[ch[cur][lson]];
            if(v[cur]<x){
                res+=cnt[cur];
                if(!ch[cur][rson]){
                    splay(cur);
                    return res+1;
                }
                cur=ch[cur][rson];
            }
            else{
                splay(cur);
                return res+1;
            }
        }
    }
}

即查询排名为 xx 的数是什么。

与 numx_rank_search() 很类似。设 xx 是剩余排名。

  1. 若 xx 大于左子树的大小，那就将 xx 减去左子树的大小，再减去当前节点的 cnt，如果此时 xx 大于 00 ，那就可以继续向右子树寻找，否则直接返回当前的值。
  2. 若 xx 不大于左子树的大小，直接向左子树寻找即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int rankx_num_search(int x){
    int cur=rt;
    while(1){
        if(x<=stre_size[ch[x][lson]]){//据说加了判断左子树非空会更严谨，实测确实会更快一点
            cur=ch[x][lson];
            continue;
        }
        x-=stre_size[ch[x][lson]]+cnt[x];
        if(x<=0){
            splay(cur);
            return cur;//也可返回 v[cur]
        }
        cur=ch[x][rson];
    }
}

del()

即删除数 xx。

这里要用到还没有提到的函数：查找前驱。

方法一

遍历查找一遍数 xx 并 splay，如果找到的节点的 cnt 大于 11，那么可以直接 cnt[cur]-- 即可。否则要合并两个子树。

如何合并？

  1. 如果两个树有空树，直接返回那个树或者空树即可。
  2. 先将左子树中的最大值 splay 到根，然后连接右子树，更新信息即可。

左子树中的最大值就是查找原根结点的前驱，即为左子树中一直向右最终遍历到的点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
void del(int x){
    numx_rank_search(x);//这一步就是查找加splay
    if(cnt[rt]>1){//易漏!
        cnt[rt]--;
        maintain(rt);
        return;
    }
    if(!ch[rt][lson]&&!ch[rt][rson]){
        clear(rt);
        rt=0;
        return;
    }
    if(!ch[rt][lson]){
        int ed_rt=rt;
        fa[ch[rt][rson]]=0;//注意是左儿子还是右儿子
        rt=ch[rt][rson];
        clear(ed_rt);//注意清理目标
        return;
    }
    if(!ch[rt][rson]){
        int ed_rt=rt;
        fa[ch[rt][lson]]=0;
        rt=ch[rt][lson];
        clear(ed_rt);
        return;
    }
    int ed_rt=rt;
    int cur=ch[rt][lson];
    while(ch[cur][rson])cur=ch[cur][rson];//查找前驱用的函数内部就差不多是这样
    splay(cur);//此时ed_rt一定没有左子树，可以较方便的删除
    ch[rt][rson]=ch[ed_rt][rson];
    fa[ch[rt][rson]]=cur;
    clear(ed_rt);
    maintain(rt);
    return;
}

方法二

把后继与前驱按顺序 splay 到根，这时原来的节点一定在后继左子树并且只有这一个节点在这棵子树中，直接断绝父子关系即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void del(int x){
    numx_rank_search(x);
    int cur1=rt,cur2=rt;
    if(ch[rt][lson]){
        cur1=ch[rt][lson];
        while(ch[cur1][rson])cur1=ch[cur1][rson];
    }
    if(ch[rt][rson]){
        cur2=ch[rt][rson];
        while(ch[cur2][lson])cur2=ch[cur2][lson];
    }
    splay(cur2);
    splay(cur1);
    if(cnt[ch[cur2][lson]]>1){
        cnt[ch[cur2][lson]]--;
        splay(ch[cur2][lson]);
        maintain(ch[cur2][lson]);
        return;
    }
    clear(ch[cur2][lson]);
    ch[cur2][lson]=0;
    maintain(cur2);
    maintain(cur1);
    return;
}

search_prenum()

即查找前驱。前面已提到核心代码，但是如果该数不在树里怎么办？

先插入，运算完了，删除即可。

1
2
3
4
5
6
7
8
9
10
11
int search_prenum(int x){
    insert(x);
    int cur=rt;
    if(ch[rt][lson]){
        cur=ch[rt][lson];
        while(ch[cur][rson])cur=ch[cur][rson];
    }
    splay(cur);
    del(x);
    return cur;
}

search_nextnum()

与前驱基本一样。

1
2
3
4
5
6
7
8
9
10
11
int search_prenum(int x){
    insert(x);
    int cur=rt;
    if(ch[rt][rson]){
        cur=ch[rt][rson];
        while(ch[cur][lson])cur=ch[cur][lson];
    }
    splay(cur);
    del(x);
    return cur;
}

Splay 到这里完结撒花！

代码整合

贴的直接是模板的 AC 代码，可能与上面的代码有些不一样的地方。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
#include<bits/stdc++.h>
using namespace std;
#define lson 0
#define rson 1
class Splay{
	public:
		int rt;//根节点编号
		int tot;//节点个数
		int fa[10000001];//各个节点的父亲
		int ch[10000001][2];//左右儿子编号
		int v[10000001];//节点权值
		int cnt[10000001];//权值出现次数
		int stre_size[10000001];//各个节点子树大小
		void maintain(int x){//在改变节点位置后，将节点 x 的 size 更新。
			if(x)stre_size[x]=(ch[x][lson]?stre_size[ch[x][lson]]:0)+(ch[x][rson]?stre_size[ch[x][rson]]:0)+cnt[x];
			return;
		}
		bool get(int x){//判断节点 x 是父亲节点的左儿子还是右儿子。
			return ch[fa[x]][rson]==x;
		}
		void clear(int x){//销毁节点 x。
			fa[x]=ch[x][lson]=ch[x][rson]=v[x]=cnt[x]=stre_size[x]=0;
			return;
		}
		//为了使 Splay 保持平衡而进行旋转操作，旋转的本质是将某个节点上移一个位置。
		void rotate(int x){
			int y=fa[x],z=fa[y],chk=get(x);
			ch[y][chk]=ch[x][chk^1];
			if(ch[y][chk])fa[ch[y][chk]]=y;
			ch[x][chk^1]=y,fa[y]=x,fa[x]=z;
			if(z)ch[z][ch[z][rson]==y]=x;
			maintain(y);
			maintain(x);
			return;
		}
		void splay(int x){//每访问一个节点 x 后都要强制将其旋转到根节点。
			for(;fa[x];rotate(x))
				if(fa[fa[x]]){
					if(get(fa[x])==get(x))rotate(fa[x]);//!!!!!
					else rotate(x);
				}
			rt=x;
			return;
		}
		/*Self-add functions are here*/
		//插入操作
		void insert(int x){
			if(!rt){//如果树空了，则直接插入根并退出。
				v[++tot]=x;
				cnt[tot]++;
				rt=tot;
				maintain(rt);
				return;
			}
			int cur=rt,buf=0;//这一次的和上一次的(fa[rt]=0) 
			while(1){
				if(v[cur]==x&&cnt[cur]){//如果当前节点的权值等于 k 则增加当前节点的大小并更新节点和父亲的信息，将当前节点进行 Splay 操作。
					cnt[cur]++;
					maintain(cur);
					maintain(buf);
					splay(cur);
					break;
				}
				buf=cur;
				cur=ch[cur][x>v[cur]];//左子树任意节点的值 < 根节点的值 < 右子树任意节点的值。
				//按照二叉查找树的性质向下找，找到空节点就插入即可
				if(!cur){
					fa[++tot]=buf;
					ch[buf][x>v[buf]]=tot;
					v[tot]=x;
					cnt[tot]++;
					maintain(tot);
					maintain(buf);
					splay(tot);
					break;
				}
			}
            return;
		}
		//查询 x 的排名
		int numx_rank_search(int x){
			int res=0,cur=rt;
			while(1){
				//如果 x 比当前节点的权值小，向其左子树查找。
				if(x<v[cur]){
					
					if(!ch[cur][lson]){
                    splay(cur);
						return res+1;
					}cur=ch[cur][lson];
					continue;
				}
				//如果 x 比当前节点的权值大，将答案加上左子树（size）和当前节点（cnt）的大小，向其右子树查找。
				res+=(ch[cur][lson]?stre_size[ch[cur][lson]]:0);
				if(x>v[cur]){
					res+=cnt[cur];
					
					if(!ch[cur][rson]){
                        splay(cur);
						return res+1;
					}cur=ch[cur][rson];
					continue;
				}
				//如果 x 与当前节点的权值相同，将答案加 1 并返回。
				//注意最后需要进行 Splay 操作。
				splay(cur);
				return res+1;
			}
		}
		//查询排名 x 的数
		int rankx_num_search(int x){
			int cur=rt;
			while(1){
				//如果左子树非空且剩余排名 x 不大于左子树的大小 size，那么向左子树查找。
				if(ch[cur][lson]&&x<=stre_size[ch[cur][lson]]){
					cur=ch[cur][lson];
					continue;
				}
				//否则将 x 减去左子树的和根的大小。
				x-=stre_size[ch[cur][lson]]+cnt[cur];
				//如果此时 x 的值小于等于 0，则返回根节点的权值
				if(x<=0){
					//注意最后需要进行 Splay 操作!!!!!!!!!
					splay(cur);
					return v[cur];
				}
				//否则继续向右子树查找。
				cur=ch[cur][rson];
			}
		}
		//删除操作
		void del(int x){
			//首先将 x 旋转到根的位置。
			numx_rank_search(x);//最后都是splay了的
			//如果 cnt[x]>1（有不止一个 x），那么将 cnt[x] 减 1 并退出
			if(cnt[rt]>1){
				cnt[rt]--;
				maintain(rt);
				return;
			}
			//否则，合并它的左右两棵子树即可。
			//如何合并？
			//设两棵树的根节点分别为 x 和 y，那么我们要求 x 树中的最大值小于 y 树中的最小值。
			//如果 x 和 y 其中之一或两者都为空树，直接返回不为空的那一棵树的根节点或空树。
			if(!ch[rt][lson]&&!ch[rt][rson]){
				clear(rt);
				rt=0;
				return;
			}
			if(!ch[rt][lson]){
                int ed_rt=rt; 
				rt=ch[rt][rson];
                fa[rt]=0;
				clear(ed_rt);
				return;
			}
			if(!ch[rt][rson]){
                int ed_rt=rt;
				rt=ch[rt][lson];
                fa[rt]=0;
				clear(ed_rt);
				return;
			}
			//否则将 x 树中的最大值 Splay 到根，然后把它的右子树设置为 y 并更新节点的信息，然后返回这个节点。
			int ed_rt=rt;
			int cur=ch[rt][lson];
			while(ch[cur][rson])cur=ch[cur][rson];
			splay(cur);
			//查找前驱(无需insert或del，所以就直接复制上来了) 
			ch[rt][rson]=ch[ed_rt][rson];
			fa[ch[rt][rson]]=rt;
			clear(ed_rt);
			maintain(rt);
			return;
		}
		//另一个思路
		//将rt的前驱与后继都Splay，此时，rt会在后继的左儿子处，直接断绝关系即可
//		void del(int x){
//			int cur=ch[rt][lson];
//			while(ch[cur][rson])cur=ch[cur][rson];
//			int curr=ch[rt][rson];
//			while(ch[cur][lson])cur=ch[cur][lson];
//			splay(curr);
//			splay(cur);
//			int temp=ch[curr][lson];
//			if(cnt[temp]>1){
//				cnt[temp]--;
//				maintain(temp);
//				splay(temp);
//			}
//			else{
//				ch[curr][lson]=0;
//				maintain(curr);
//				maintain(cur);
//			}
//			return;
//		}
		//查询前驱
		int search_prenum(int x){
			//前驱定义为小于 x 的最大的数
			//转化:
			//将 x 插入（此时 x 已经在根的位置了）
			insert(x);
			//前驱即为 x 的左子树中最右边的节点
			int cur=ch[rt][lson];
			if(!cur)return cur;//没有这种数 
			while(ch[cur][rson])cur=ch[cur][rson]/*,cout<<v[cur]<<" test"<<endl;*/;
			splay(cur);
            
			del(x);//最后将 x 删除即可。
			return cur;
		}
		//查询后继:与前驱极其类似
		int search_nextnum(int x){
			//后继定义为大于 x 的最小的数
			//转化:
			//将 x 插入（此时 x 已经在根的位置了）
			insert(x);
			//后继即为 x 的右子树中最左边的节点
			int cur=ch[rt][rson];
			if(!cur)return cur;//没有这种数 
			while(ch[cur][lson])cur=ch[cur][lson];
			splay(cur);
			del(x);//最后将 x 删除即可。
			return cur;
		}
}tree;

int main()
{
//	freopen("P6136_5.in","r",stdin);
    ios::sync_with_stdio(0);
    cin.tie(0);
	int n,m,op,x,last=0,ans=0;
	cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>x;
        tree.insert(x);
    }
    while(m--){
		cin>>op;
		if(op==1){
			cin>>x;
			tree.insert(x^last);
		}
		if(op==2){
			cin>>x;
			tree.del(x^last);
		}
		if(op==3){
			cin>>x;
			last=tree.numx_rank_search(x^last);
            ans^=last;
		}
		if(op==4){
			cin>>x;
			last=tree.rankx_num_search(x^last);
            ans^=last;
		}
		if(op==5){
			cin>>x;
			last=tree.v[tree.search_prenum(x^last)];
            ans^=last;
		}
		if(op==6){
			cin>>x;
			last=tree.v[tree.search_nextnum(x^last)];
            ans^=last;
		}
//		if(!(m%10000))cout<<m<<endl;
	}
    cout<<ans<<endl;
    return 0;
}

模板地址：here

从 Splay 到 LCT

鸽…