Simple-Algos-Notes

二分

分为二分序列，二分数据结构，和二分答案。

需要满足有单调性才能二分。如果是一个凸壳可以三分。

二分答案

例题：P6069

注意这题对于方差何时最小是不能贪心处理的。

首先要排序，然后二分剩下的人数 $k$，枚举各个长为 $k$ 的区间内的方差即可。需要推一下方差式子，时间复杂度 $O(n\log n)$。

可以尺取做到 $O(n)$。

排序是为了选取的数连续，因为一些不连续的数向序列中连续的数转移一定不劣。

// Problem: P6069 『MdOI R1』Group
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P6069
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int n;
#define int long long
int a[200005];__int128 s[200005],m[200005];long long k,p;

bool check(int x){
	for(int i=1;i<=n-x+1;i++){
		//cout<<((m[i+x-1]-m[i-1])-1.0*(s[i+x-1]-s[i-1])*(s[i+x-1]-s[i-1])/x)<<"\n";
		if(k>=((m[i+x-1]-m[i-1])-1.0*(s[i+x-1]-s[i-1])*(s[i+x-1]-s[i-1])/x))return 1;
	}
	return 0;
}

signed main(){
	ios::sync_with_stdio(0);
	cin>>n>>k;
	for(int i=1;i<=n;i++)cin>>a[i];
	sort(a+1,a+n+1);
	//for(int i=1;i<=n;i++)cout<<a[i]<<" ";
	//cout<<endl;
	for(int i=1;i<=n;i++)s[i]=s[i-1]+a[i],m[i]=a[i]*a[i]+m[i-1];
	int l=1,r=n,ans=1;
	while(l<=r){
		int mid=(l+r)/2;
		if(check(mid))ans=mid,l=mid+1;
		else r=mid-1;
	}
	cout<<n-ans;
	return 0;
}

例题：P2898

比较考思维。

首先，二分答案。

然后考虑如何设计出 $check$ 函数。

首先，题中的 矛盾 有两个条件：

1. 当前区间与其他区间形成 不可能合法 的情况。
2. 当前区间与其他相同权值的区间无交。

第二种情况求区间交，简单，直接求左端点最大值和右端点最小值即可。

第一种情况考虑用边权从大到小排序，然后显然如果该区间已经发现被之前的区间覆盖过了，那么直接矛盾，退出。然后将该边权下的所有区间进行覆盖。可以用线段树维护。

然后你会发现样例也过不去。

细心发现样例权值为 $7$ 的区间是 $[1,10]$ 和 $[5,19]$ 的，意味着 $[5,10]$ 这个区间里面一定有 $7$。所以使用这个区间，即区间交，进行询问。

然后就能 AC 了。

// Problem: P2898 [USACO08JAN] Haybale Guessing G
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2898
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int n,q;
int xds[4000001],lazy[4000001];
void init(){
	for(int i=1;i<=4*n;i++)xds[i]=lazy[i]=0;
	return;
}
void pushup(int now){
	xds[now]=min(xds[now<<1],xds[now<<1|1]);
	return;
}
void pushdown(int now,int l,int r){
	if(lazy[now]){
		xds[now<<1]=lazy[now];
		xds[now<<1|1]=lazy[now];
		lazy[now<<1]=lazy[now];
		lazy[now<<1|1]=lazy[now];
		lazy[now]=0;
	}
	return;
}
void mdf(int now,int l,int r,int sl,int sr,int v){
	if(l==sl&&r==sr){
		lazy[now]=v;
		xds[now]=v;
		return;
	}
	pushdown(now,l,r);
	int mid=(l+r)/2;
	if(sl<=mid)mdf(now<<1,l,mid,sl,min(sr,mid),v);
	if(sr>mid)mdf(now<<1|1,mid+1,r,max(sl,mid+1),sr,v);
	pushup(now);
	return;
}
int qmin(int now,int l,int r,int sl,int sr){
	if(l==sl&&r==sr)return xds[now];
	pushdown(now,l,r);
	int mid=(l+r)/2,res=1e9;
	if(sl<=mid)res=min(res,qmin(now<<1,l,mid,sl,min(sr,mid)));
	if(sr>mid)res=min(res,qmin(now<<1|1,mid+1,r,max(sl,mid+1),sr));
	pushup(now);
	return res;
}

struct K{
	int l,r,w;
	bool operator < (const K &a) const{
		return w>a.w;
	}
}A[30001],temp[30001];
bool check(int x){
	init();
	for(int i=1;i<=x;i++)temp[i]=A[i];
	temp[x+1].w=0;
	sort(temp+1,temp+x+1);
	//mdf(1,1,n,temp[1].l,temp[1].r,temp[1].w);
	int last=1;
	for(int i=1;i<=x+1;i++){
		if(temp[last].w!=temp[i].w){
			int L=last,R=last;
			if(i-last!=1){
				for(int o=last+1;o<i;o++){
					if(temp[o].l>temp[L].l)L=o;
					if(temp[o].r<temp[R].r)R=o;
				}
				if(temp[R].r<temp[L].l)return 0;
			}
			//cout<<last<<" "<<qmin(1,1,n,temp[L].l,temp[R].r)<<" "<<temp[i].w<<"\n";
			if(qmin(1,1,n,temp[L].l,temp[R].r))return 0;
			for(int k=last;k<i;k++)mdf(1,1,n,temp[k].l,temp[k].r,temp[k].w);
			last=i;
		}
	}
	return 1;
}

int main(){
	ios::sync_with_stdio(0);
	cin>>n>>q;
	for(int i=1;i<=q;i++)cin>>A[i].l>>A[i].r>>A[i].w;
	int l=1,r=q,ans=0;
	while(l<=r){
		int mid=(l+r)/2;
		if(check(mid))l=mid+1;
		else ans=mid,r=mid-1;
		// cout<<l<<" "<<r<<"\n";
	}
	cout<<ans;
	
	return 0;
}

例题：P2498

处理出圆心距，然后二分答案，如果两圆有交，则两圆心连边，若圆与边界有交，则圆心与边界的虚点连边，用 BFS 判断是否完全隔离。

// Problem: P2498 [SDOI2012] 拯救小云公主
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2498
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int n,r,c;
struct po{
	int x,y;
	long long getdis(const po &a){//ping fang ed.
		return 1ll*(a.x-x)*(a.x-x)+1ll*(a.y-y)*(a.y-y);
	}
}P[10001];
struct line{
	int to,link;
}E[20000001];
int head[10001],tot;
void init(){
	for(int i=1;i<=tot;i++)E[i]={0,0};
	for(int i=1;i<=n+4;i++)head[i]=0;
	tot=0;
	return;
}
void addE(int u,int v){
	E[++tot].link=head[u];
	E[tot].to=v;
	head[u]=tot;
	// assert(tot<=10000000);
	return;
}
int vis[10001];
queue<int> q;
//t => n+2|n+4
bool BFS(int s){
	for(int i=1;i<=n+5;i++)vis[i]=0;
	q.push(s);
	while(!q.empty()){
		int u=q.front();q.pop();
		//cerr<<s<<" "<<u<<"\n";
		vis[u]=1;
		if(u==n+2||u==n+4){
			while(!q.empty())q.pop();
			return 1;
		}
		for(int i=head[u];i;i=E[i].link){
			if(!vis[E[i].to])q.push(E[i].to);
		}
	}
	while(!q.empty())q.pop();
	return 0;
}


//shang:n+1,xia:n+2,zuo:n+3,you:n+4
//shang->you|xia => n+1 -> n+2|n+4
//zuo->you|xia => n+3 -> n+2|n+4
bool check(double x){
	init();
	for(int i=1;i<=n;i++){
		for(int j=1;j<i;j++){
			if(P[i].getdis(P[j])<4*x*x)addE(i,j),addE(j,i);
		}
		if(P[i].x<x+1)addE(n+3,i),addE(i,n+3);//zuo//Caution!!! x+1!!!
		if(P[i].x+x>r)addE(i,n+4),addE(n+4,i);//you
		if(P[i].y<x+1)addE(i,n+2),addE(n+2,i);//xia
		if(P[i].y+x>c)addE(n+1,i),addE(i,n+1);//shang
	}
	if(BFS(n+1))return 0;
	return !BFS(n+3);
}

int main(){
	ios::sync_with_stdio(0);
	cin>>n>>r>>c;
	for(int i=1;i<=n;i++){
		cin>>P[i].x>>P[i].y;
	}
	double L=0.5,R=max(r,c);
	while(R-L>=0.001){
		double mid=(L+R)/2;
		if(check(mid))L=mid;
		else R=mid;
		//cerr<<"ZFYNBNBNB! "<<L<<" "<<R<<" "<<clock()<<"\n";
	}
	cout<<fixed<<setprecision(2)<<L;
	return 0;
}

例题：P1663

首先有一个显然的 $O(n^2)$ 做法：将斜率在原点左右两侧的直线求交点即可。

考虑如何用 $O(n \log n)$ 解决。

二分答案，预处理出直线解析式，然后对于每条直线，求与直线 $y=mid$ 的交点的纵坐标。如果 $k_{now}=0$，则 $mid>b_{now}$ 合法；然后把 $k_{now}>0$ 的直线当做右端点，$k_{now}<0$ 的直线当做左端点，然后求区间交即可。如果该区间存在，那么合法。

// Problem: P1663 山
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1663
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int n;
int x[5001],y[5001];
long double k[5001];
long double b[5001];

bool check(long double y){
	long double l=0,r=1e5;
	for(int i=1;i<n;i++){
		// cout<<k[i]<<" "<<b[i]<<"\n";
		if(k[i]==0){
			if(y<b[i])return 0;
		}
		else if(k[i]>0){
			r=fmin(r,(y-b[i])/k[i]);
			// cout<<r<<" R\n";
		}
		else l=fmax(l,(y-b[i])/k[i]);//,cout<<l<<" L\n";
	}
	return l<=r;
}

int main(){
	ios::sync_with_stdio(0);
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>x[i]>>y[i];
		if(i>1){
			k[i-1]=1.0*(y[i]-y[i-1])/(x[i]-x[i-1]);
			b[i-1]=-k[i-1]*x[i]+y[i];
		}
	}
	// Seg Cnt:n-1
	long double L=0,R=1e6;
	while(R-L>=0.000001){
		long double mid=(L+R)/2;
		if(check(mid))R=mid;
		else L=mid;
	}
	cout<<fixed<<setprecision(2)<<L;
	return 0;
}

例题：P1485

考虑二分答案。

用差分拆出平方即可。

细节巨多。

// Problem: P1485 火枪打怪
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1485
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,k;
int m[500005],t[500005];
int _1[500005],_2[500005],_3[500005],_4[500005];
bool check(int x){
	//cerr<<x<<"\n";
	int C=0;
	int S=sqrt(x);
	for(int i=0;i<=n+1;i++)_1[i]=_2[i]=_3[i]=_4[i]=0,t[i]=m[i];
	for(int i=n;i>=1;i--){
		//cerr<<_1[i]<<" "<<_2[i]<<" "<<_3[i]<<" "<<_4[i]<<"\n";
		_4[i]+=_4[i+1];
		_3[i]=_3[i]+_3[i+1]+_4[i+1];
		_2[i]=_2[i]+_3[i]+_2[i+1];
		_1[i]+=_1[i+1];
		//cerr<<_1[i]<<" "<<_2[i]<<" "<<_3[i]<<" "<<_4[i]<<"\n";
		t[i]-=_1[i]-_2[i];
		int lef=0;
		if(t[i]>=0)lef=t[i]/x+1;
		_4[i]+=lef;
		if(i-1>0)_4[i-1]+=lef;
		_1[i]+=lef*x;
		C+=lef;
		//cerr<<i<<" "<<C<<" "<<t[i]<<" "<<lef<<" Gino\n";
		if(i-S-1>0)_4[i-S-1]-=2*lef,_1[i-S-1]-=lef*x,_2[i-S-1]-=(S)*(S)*lef,_3[i-S-1]-=lef*(2*S+1);
	}
	return C<=k;
}
signed main(){
	ios::sync_with_stdio(0);
	// _4[16]=1,_4[15]=2;
	// for(int i=16;i>=1;i--){
		// _4[i]+=_4[i+1];
		// _3[i]=_3[i+1]+_4[i];
		// _2[i]=_2[i]+_3[i]+_2[i+1];
		// _1[i]+=_1[i+1];
// 		
		// //cerr<<_1[i]<<" "<<_2[i]<<" "<<_3[i]<<" "<<_4[i]<<"\n";
	// }
	cin>>n>>k;
	for(int i=1;i<=n;i++)cin>>m[i];
	int l=0,r=1e16,ans=0;
	while(l<=r){
		int mid=(l+r)/2;
		if(check(mid))r=mid-1,ans=mid;
		else l=mid+1;
		//cerr<<l<<" "<<r<<" "<<ans<<" ww\n";
	}
	// check(6);
	cout<<ans;
	return 0;
}

例题：P1281

简单的二分答案。

考虑倒着做区间划分即可。

// Problem: P1281 书的复制
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1281
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[501],x[501],y[501];

bool check(int x){
	int sum=0,C=1;
	for(int i=1;i<=n;i++){
		if(a[i]>x)return 0;
		if(sum+a[i]>x)C++,sum=a[i];
		else sum+=a[i];
	}
	return C<=m;
}

int main(){
	ios::sync_with_stdio(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>a[i];
	reverse(a+1,a+n+1);
	int l=1,r=1e9,ans=0;
	while(l<=r){
		int mid=(l+r)/2;
		if(check(mid))r=mid-1,ans=mid;
		else l=mid+1;
	}
	int S=0,K=1;
	x[1]=1;
	for(int i=1;i<=n;i++){
		if(S+a[i]>ans)y[K]=i-1,x[++K]=i,S=a[i];
		else S+=a[i];
	}
	y[K]=n;
	reverse(y+1,y+m+1),reverse(x+1,x+m+1);
	for(int i=1;i<=m;i++)cout<<n-y[i]+1<<" "<<n-x[i]+1<<"\n";
	return 0;
}

二分查找

就是想对于一个集合 $S$，想从中找到一个值为 $t$ 的元素。如果保证集合 $S$ 在某些特征下有序，且可以查询一个子集中是否有 $t$，那么可以二分集合 $S$，通过 $mid$ 值与 $t$ 值的比较或者询问 $[l,mid]$ 区间内是否有 $t$ 来判断 $t$ 是在左区间还是右区间即可。

通常交互题要用这种二分来询问。

例题：P7345

这道题的二分方式有点厉害。

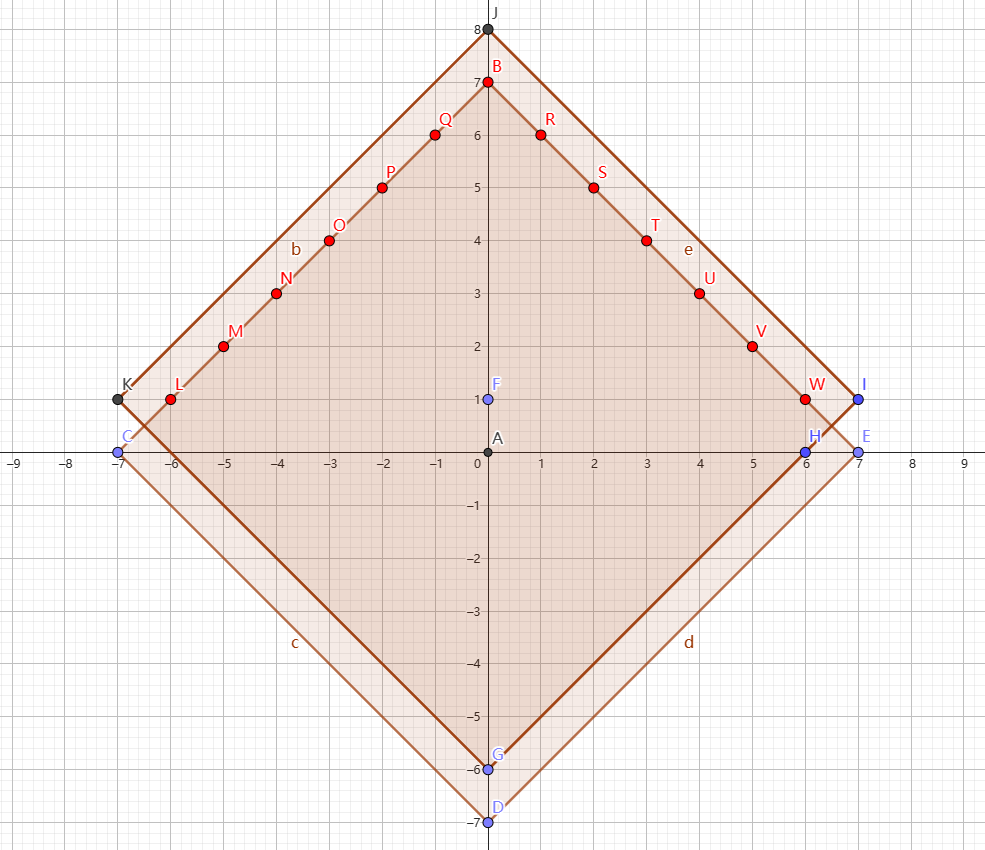
首先，这道题是一道求曼哈顿距离为 $x$ 的点集中一个特定的点。

它是一个正方形：

可以发现，如果取 $(x_0,y_0+1)$ 询问，可以筛掉近 $\left\lfloor\frac{P}{2}\right\rfloor$ 的点，其中 $P$ 是点集大小。

第一步想到就好办了。

第二次询问就是询问是在左边的线上还是在右边的线上，然后二分即可。

也可以第一次就询问四条边上是哪条边，但是 $MAX$ 卡的很紧，所以只能用上面那种方法。

// Problem: P7345 【DSOI 2021】吟唱的金色花海
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P7345
// Memory Limit: 128 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int q,x_0,y_0,k,t;
bool T;
void Q(int X,int Y){
	cout<<0<<" "<<X<<" "<<Y<<"\n";
	cout.flush();
	cin>>T;
	return;
}


int main(){
	ios::sync_with_stdio(0);
	cin>>q;
	while(q--){
		cin>>t>>x_0>>y_0>>k;
		int l,r,ans=0;
		Q(x_0,y_0+1);
		if(T==1){//up
			Q(x_0-t,y_0+t);//? up-left
			if(T==1){//up-left
				l=x_0-t,r=x_0;
				ans=x_0;
				while(l<=r){
					int mid=(l+r)/2;
					Q(mid-t,t-x_0+mid+y_0);
					if(T)ans=mid,r=mid-1;
					else l=mid+1;
				}
				cout<<1<<" "<<ans<<" "<<t-x_0+ans+y_0<<"\n";
			}else{//up-right
				l=x_0,r=x_0+t;
				ans=x_0;
				while(l<=r){
					int mid=(l+r)/2;
					Q(mid+t,t-mid+x_0+y_0);
					if(T)ans=mid,l=mid+1;
					else r=mid-1;
				}
				cout<<1<<" "<<ans<<" "<<t-ans+x_0+y_0<<"\n";
			}
		}else{//down
			Q(x_0-t,y_0-t);//? down-left
			if(T==1){//down-left
				l=x_0-t,r=x_0;
				ans=x_0;
				while(l<=r){
					int mid=(l+r)/2;
					Q(mid-t,-(t-x_0+mid)+y_0);
					if(T)ans=mid,r=mid-1;
					else l=mid+1;
				}
				cout<<1<<" "<<ans<<" "<<-(t-x_0+ans)+y_0<<"\n";	
			}else{//down-right
				l=x_0,r=x_0+t;
				ans=x_0;
				while(l<=r){
					int mid=(l+r)/2;
					Q(mid+t,-(t-mid+x_0)+y_0);
					if(T)ans=mid,l=mid+1;
					else r=mid-1;
				}
				cout<<1<<" "<<ans<<" "<<-(t-ans+x_0)+y_0<<"\n";
			}
		}
	}
	return 0;
}

在数据结构上二分

最经典的问题就是全局第 $k$ 小。考虑建权值线段树，在权值线段树上像平衡树一样查找就行了。

例题大多是线段树或树状数组上二分。

P5579

考虑用线段树维护区间加特定数列（前缀和优化），由于序列有单调性，可以使用线段树上二分找到第一个大于 $k$ 的数（类似于 upper_bound，维护区间最大值即可），然后区间赋值统计答案就行了。

注意由于 cut 标记打在了 grow 标记的后面，所以 cut 更具有时效性，pushdown 时，先处理 cut，再处理 grow。

// Problem: P5579 [PA2015] Siano
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5579
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m;
int a[500005];
int xds[2000005],sum[2000005],sta[2000005],tagc[2000005];
int pre[500005];
void pushup(const int now){
	xds[now]=max(xds[now<<1],xds[now<<1|1]);
	sum[now]=sum[now<<1]+sum[now<<1|1];
	return;
}
int id[500005];
void bulid(const int now,const int l,const int r){
	tagc[now]=-1;
	if(l==r)return id[l]=now,void();
	const int mid=(l+r)/2;
	bulid(now<<1,l,mid);
	bulid(now<<1|1,mid+1,r);
	return;
}
void cut(const int now,const int l,const int r,const int k){
	tagc[now]=xds[now]=k;
	sum[now]=k*(r-l+1);
	sta[now]=0;
	return;
}
void grow(const int now,const int l,const int r,const int cl){
	sum[now]+=(pre[r]-pre[l-1])*cl;
	sta[now]+=cl;
	xds[now]+=a[r]*cl;
	return;
}
void pushdown(const int now,const int l,const int r){
	const int mid=(l+r)/2;
	if(tagc[now]!=-1){
		cut(now<<1,l,mid,tagc[now]);
		cut(now<<1|1,mid+1,r,tagc[now]);
		tagc[now]=-1;
	}
	if(sta[now]){
		grow(now<<1,l,mid,sta[now]);
		grow(now<<1|1,mid+1,r,sta[now]);
		sta[now]=0;
	}
	return;
}
int mdf(const int now,const int l,const int r,const int sl,const int sr,const int k){
	// if(sr<sl)return 0;
	if(l==sl&&r==sr){
		int ed=sum[now];
		// cout<<l<<" "<<r<<" "<<ed<<"\n";
		cut(now,l,r,k);
		return ed-sum[now];
	}
	const int mid=(l+r)/2;
	int res=0;
	pushdown(now,l,r);
	if(sl<=mid)res+=mdf(now<<1,l,mid,sl,min(sr,mid),k);
	if(sr>mid)res+=mdf(now<<1|1,mid+1,r,max(sl,mid+1),sr,k);
	pushup(now);
	return res;
}
int find(const int now,const int l,const int r,const int k){
	if(l==r)return l;
	pushdown(now,l,r);
	const int mid=(l+r)/2;
	int res;
	if(k>xds[now<<1])res=find(now<<1|1,mid+1,r,k);
	else res=find(now<<1,l,mid,k);
	pushup(now);
	return res;
}
signed main(){
	ios::sync_with_stdio(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>a[i];
	sort(a+1,a+n+1);
	for(int i=1;i<=n;i++)pre[i]=pre[i-1]+a[i];
	int lst=0,x,y;
	for(int i=1;i<=m;i++){
		cin>>x>>y;
		grow(1,1,n,x-lst);
		lst=x;
		// cout<<find(1,1,n,y)<<" test\n";
		if(xds[1]<=y){
			cout<<0<<"\n";
			continue;
		}
		cout<<mdf(1,1,n,find(1,1,n,y),n,y)<<"\n";
	}
	return 0;
}

P3224

此题线段树上二分无法通过（常数太大了），故使用树状数组二分。

这种二分类似于倍增。观察上面图，其实发现树状数组节点记录的信息就是 $[i-\operatorname{lowbit}(i)+1,i]$，如果用更通俗的语言来讲，对于从 $0$ 开始到 $\left\lfloor\log n\right\rfloor$ 的所有 $i$，第 $2^i$ 个节点记录的是前 $2^i$ 个元素所有的信息。如果从该节点拓展出一个节点 $j$ 满足 $j<i$，那么节点 $2^j+2^i$ 记录的信息就是 $[2^i+1,2^i+2^j]$ 区间内的所有信息，那么用类似于倍增的算法从 $\left\lfloor\log n\right\rfloor$ 开始向下枚举到 $0$ 就能找到位置了。

本题则较为复杂。不难发现当 冰 <= 场地 <= 火 时，如果场地的温度在滑动，那么满足火系的能量和是后缀和，冰系的能量和是前缀和，那么我们只需要二分出两条曲线的交点所在最小区间左右端点，然后再对于其中最大值找到最大的温度满足值仍最大即可。

细节较多，具体可以参考代码。

// Problem: P6619 [省选联考 2020 A/B 卷] 冰火战士
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P6619
// Memory Limit: 512 MB
// Time Limit: 3000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int tice[2000005],tfire[2000005];
int op,t,x,y,q;
int id[2000005],_C[2000005],ene[2000005];
int temp[2000005],tcnt;
const int _=2e6+1;
int lowbit(int x){
	return x&-x;
}
void mdfice(int x,int v){
	while(x<=_-1){
		tice[x]+=v;
		x+=lowbit(x);
	}
	return;
}
void mdffire(int x,int v){
	while(x<=_-1){
		tfire[x]+=v;
		x+=lowbit(x);
	}
	return;
}
int qice(int x){
	int res=0;
	while(x>0){
		res+=tice[x];
		x-=lowbit(x);
	}
	return res;
}
int qfire(int x){
	int res=0;
	while(x>0){
		res+=tfire[x];
		x-=lowbit(x);
	}
	return res;
}
int org[_+4],O[_+4],buc[_+4];
int main(){
	ios::sync_with_stdio(0);
	cin>>q;
	for(int i=1;i<=q;i++){
		cin>>op>>t;
		if(op==1){
			cin>>x>>y;
			id[i]=t;
			_C[i]=x;
			O[i]=x;
			ene[i]=y;
			temp[++tcnt]=_C[i];
		}
		else{
			id[i]=-1;
			_C[i]=t;
		}
	}
	sort(temp+1,temp+tcnt+1);
	tcnt=unique(temp+1,temp+tcnt+1)-temp-1;	
	for(int i=1;i<=q;i++){
		if(id[i]>=0)_C[i]=lower_bound(temp+1,temp+tcnt+1,_C[i])-temp,org[_C[i]]=O[i];
	}
	int zfy=0;
	for(int i=q;i>=1;i--){
		if(org[i]!=0)zfy=org[i];
		else org[i]=zfy;
	}
	for(int i=1;i<=q;i++){
		// cerr<<org[_C[i]]<<"\n";
		if(id[i]==-1){
			if(id[_C[i]])mdffire(_C[_C[i]],-ene[_C[i]]),buc[_C[_C[i]]]-=ene[_C[i]];
			else mdfice(_C[_C[i]],-ene[_C[i]]);
		}
		else if(id[i]){
			mdffire(_C[i],ene[i]);
			buc[_C[i]]+=ene[i];
		}
		else{
			mdfice(_C[i],ene[i]);
		}
		int std=qfire(_-1);
		if(std==0||qice(_-1)==0){cout<<"Peace\n";continue;}
		int now=0,ICE=0,FIRE=0;
		for(int o=20;o>=0;o--){
			int ptt=now+(1<<o);
			if(ptt<=q&&tice[ptt]+ICE<=std-tfire[ptt]-FIRE+buc[ptt])now=ptt,FIRE+=tfire[ptt],ICE+=tice[ptt];
			// cerr<<now<<" "<<ICE<<" "<<FIRE<<" "<<tice[ptt]+ICE<<" "<<std-tfire[ptt]-FIRE+buc[ptt]<<" "<<" in\n";
		}
		int M=min(std-qfire(now)+buc[now],qice(now));
		int test=min(std-qfire(now+1)+buc[now+1],qice(now+1));
		// cerr<<"\n";
		// cerr<<i<<"\n";
		// cerr<<std<<" "<<now<<" "<<ICE<<" "<<FIRE<<"\n";
		// cerr<<test<<"\n";
		if(test==0&&M==0){
			cout<<"Peace\n";
			continue;
		}
		// cerr<<"\n";
		if(test>=M){
			// cout<<org[now+1]<<" "<<test<<"\n";
			int ans=0;
			ICE=0,FIRE=0;
			for(int o=20;o>=0;o--){
				int ptt=ans+(1<<o);
				if(ptt<=q&&std-tfire[ptt]-FIRE+buc[ptt]>=test)ans=ptt,FIRE+=tfire[ptt];
			}
			// cerr<<"! "<<ans<<"\n";
			cout<<org[ans]<<" "<<test*2<<"\n";
		}
		else cout<<org[now]<<" "<<M*2<<"\n";
	}
	return 0;
}

CF1439C

很好的一道线段树上二分的题。

我们分操作讨论线段树上的操作。

对于操作一，考虑它不会改变区间单调性，那么可以二分找出第一个严格比 $y$ 小的数的位置，然后对于该位置到 $x$ 的区间进行区间赋值操作就行了，时间复杂度 $O(\log n)$。

对于操作二，维护区间和，每次暴力遍历左右子树寻找区间的最小值位置，然后对于这个位置的子区间进行对当前数减去子区间的和的操作。不难发现这种位置每次最多有 $O(\log n)$ 个，然后由于序列的单调性，每次当前数至少减半，那么时间复杂度为 $O(\log n\log V)$，总时间复杂度为 $O(q\log n\log V)$。

// Problem: Greedy Shopping
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF1439C
// Memory Limit: 250 MB
// Time Limit: 3000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=2e5+5;
int xds[maxn<<2];//sum num
int mi[maxn<<2];//min num
int qy;//querying y
int tag[maxn<<2];//lazy tag for assign operation
void pushup(int now){
	xds[now]=xds[now<<1]+xds[now<<1|1];
	mi[now]=min(mi[now<<1],mi[now<<1|1]);
	return;
}
void pushdown(int now,int l,int r){
	if(tag[now]){
		int mid=(l+r)/2;
		tag[now<<1]=tag[now];
		tag[now<<1|1]=tag[now];
		xds[now<<1]=tag[now]*(mid-l+1);
		xds[now<<1|1]=tag[now]*(r-mid);
		mi[now<<1]=tag[now];
		mi[now<<1|1]=tag[now];
		tag[now]=0;
	}
	return;
}
int a[maxn];
void bulid(int now,int l,int r){
	if(l==r)return mi[now]=xds[now]=a[l],void();
	int mid=(l+r)/2;
	mi[now]=1e9;
	bulid(now<<1,l,mid);
	bulid(now<<1|1,mid+1,r);
	pushup(now);
	return;
}
int find(int now,int l,int r,int v){
	//Querying upperbound_greater_int
	if(l==r)return l;
	int mid=(l+r)/2,res=0;
	pushdown(now,l,r);
	if(mi[now<<1]<v)res=find(now<<1,l,mid,v);
	else res=find(now<<1|1,mid+1,r,v);
	pushup(now);
	return res;
}
void mdf(int now,int l,int r,int sl,int sr,int v){
	//assign operation executor
	//cerr<<now<< ' ' << l << ' ' << r << ' ' << sl << ' ' << sr <<"\n";
	if(l==sl&&r==sr)return xds[now]=v*(r-l+1),mi[now]=v,tag[now]=v,void();
	int mid=(l+r)/2;
	pushdown(now,l,r);
	if(sl<=mid)mdf(now<<1,l,mid,sl,min(sr,mid),v);
	if(sr>mid)mdf(now<<1|1,mid+1,r,max(sl,mid+1),sr,v);
	pushup(now);
	return;
}
int query(int now,int l,int r,int st){
	// cerr << now<<" "<<l<<" "<<r<<" "<<qy<<" "<<mi[now] << endl;
	//Deal with operator 2 -> Search for the operation range and count
	if(r<st||qy<mi[now])return 0;
	if(l>=st&&qy>=xds[now]){
		qy-=xds[now];
		return r-l+1;
	}
	// if(l==r)return 0;
	int mid=(l+r)/2,res=0;
	pushdown(now,l,r);
	if(mid>=st)res+=query(now<<1,l,mid,st);
	res+=query(now<<1|1,mid+1,r,st);
	pushup(now);
	return res;
}
int n,m;

signed main(){
	ios::sync_with_stdio(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>a[i];
	bulid(1,1,n);
	int op,x;
	while(m--){
		cin>>op>>x>>qy;
		//cerr<<m<<'\n';
		if(op==1){
			int s=find(1,1,n,qy);
			if(s>x)continue;
			mdf(1,1,n,s,x,qy);
		}
		else{
			cout<<query(1,1,n,x)<<"\n";
		}
	}
	return 0;
}

CF1705E

首先开权值线段树。维护每一位的二进制加减过程。

对于每一次操作，分为删除一个数再加上一个数。

删除数时，如果当前位值为 $1$，直接删除即可；如果值为 $0$，则需要线段树上二分出从当前位开始向右第一个值为 $1$ 的位，将此位设置为 $0$，然后将左侧区间赋值为 $1$。

加入同理。答案就是右侧第一个 $1$ 的位置。

二分的时候需要维护区间是否有 $0$ 或者 $1$，其他正常在子区间二分即可，单次询问最坏时间复杂度为 $O(\log n+\log n)=O(\log n)$，其中第一个 $\log n$ 是在寻找子区间中第一个有 $0$ 或 $1$ 的区间，第二个 $\log n$ 是在寻找该区间中最小的 $0$ 或 $1$。总时间复杂度是较大常数的 $O(q\log n)$。

// Problem: Mark and Professor Koro
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF1705E
// Memory Limit: 250 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+5;
int a[maxn];
bool xds0[maxn<<3],xds1[maxn<<3];
bool lazy0[maxn<<3],lazy1[maxn<<3];
void pushup(int now){
	xds1[now]=xds1[now<<1]|xds1[now<<1|1];
	xds0[now]=xds0[now<<1]|xds0[now<<1|1];
	return;
}
void pushdown(int now,int l,int r){
	assert((!lazy1[now]||!lazy0[now]));
	if(lazy0[now]){
		xds0[now<<1]=1;
		xds1[now<<1]=0;
		lazy0[now<<1]=1;
		lazy1[now<<1]=0;
		xds0[now<<1|1]=1;
		xds1[now<<1|1]=0;
		lazy0[now<<1|1]=1;
		lazy1[now<<1|1]=0;
		lazy0[now]=0;
	}
	if(lazy1[now]){
		xds0[now<<1]=0;
		xds1[now<<1]=1;
		lazy0[now<<1]=0;
		lazy1[now<<1]=1;
		xds0[now<<1|1]=0;
		xds1[now<<1|1]=1;
		lazy0[now<<1|1]=0;
		lazy1[now<<1|1]=1;
		lazy1[now]=0;
	}
	return;
}
int find0(int now,int l,int r,int st){
	if(r<st||xds0[now]==0)return 1e9;
	if(l>=st){
		if(l==r)return xds1[now]=1,xds0[now]=0,l;
		pushdown(now,l,r);
		int mid=(l+r)/2;
		int res=0;
		if(xds0[now<<1])res=find0(now<<1,l,mid,st);
		else res=find0(now<<1|1,mid+1,r,st);
		pushup(now);
		return res;
	}
	pushdown(now,l,r);
	int mid=(l+r)/2,res=1e9;
	if(mid>=st)res=min(res,find0(now<<1,l,mid,st));
	if(res!=1e9)return pushup(now),res;
	res=min(res,find0(now<<1|1,mid+1,r,st));
	pushup(now);
	return res;
}
int find1(int now,int l,int r,int st){
	if(r<st||xds1[now]==0)return 1e9;
	if(l>=st){
		if(l==r)return xds0[now]=1,xds1[now]=0,l;
		pushdown(now,l,r);
		int mid=(l+r)/2;
		int res=0;
		if(xds1[now<<1])res=find1(now<<1,l,mid,st);
		else res=find1(now<<1|1,mid+1,r,st);
		pushup(now);
		return res;
	}
	pushdown(now,l,r);
	int mid=(l+r)/2,res=1e9;
	if(mid>=st)res=min(res,find1(now<<1,l,mid,st));
	if(res!=1e9)return pushup(now),res;
	res=min(res,find1(now<<1|1,mid+1,r,st));
	pushup(now);
	return res;
}
void mdf(int now,int l,int r,int sl,int sr,bool v){
	if(l==sl&&r==sr){
		if(v)xds1[now]=1,xds0[now]=0,lazy1[now]=1,lazy0[now]=0;
		else xds0[now]=1,xds1[now]=0,lazy0[now]=1,lazy1[now]=0;
		return;
	}
	pushdown(now,l,r);
	int mid=(l+r)/2;
	if(sl<=mid)mdf(now<<1,l,mid,sl,min(mid,sr),v);
	if(sr>mid)mdf(now<<1|1,mid+1,r,max(mid+1,sl),sr,v);
	pushup(now);
	return;
}
int n,m;
const int _=4e5;
void insert(int v){
	int nxt=find0(1,1,_,v);
	//cerr<<nxt<<" "<<v<<"\n";
	if(nxt==v)return;
	mdf(1,1,_,v,nxt-1,0);
	return;
}
void del(int v){
	int nxt=find1(1,1,_,v);
	//cerr<<nxt<<" "<<v<<" delling\n";
	if(nxt==v)return;
	mdf(1,1,_,v,nxt-1,1);
	return;
}
void init(){
	lazy0[1]=1;
	xds0[1]=1;
	return;
}
int getans(int now,int l,int r){
	if(l==r)return l;
	pushdown(now,l,r);
	int mid=(l+r)/2,res=0;
	if(xds1[now<<1|1])res=getans(now<<1|1,mid+1,r);
	else res=getans(now<<1,l,mid);
	pushup(now);
	return res;
}
int main(){
	ios::sync_with_stdio(0);
	cin>>n>>m;
	init();
	for(int i=1;i<=n;i++){
		cin>>a[i];
		insert(a[i]);
	}
	int x,y;
	while(m--){
		cin>>x>>y;
		del(a[x]);
		insert(y);
		a[x]=y;
		cout<<getans(1,1,_)<<"\n";
	}
	return 0;
}

离线二分

分为 CDQ 分治和整体二分。

CDQ 分治

严格意义上，这只是一种分治的思想。

在处理询问时，可以将左区间和右区间先分开处理，然后再处理跨过了 $mid$ 的部分。

注意，当题中有时间顺序要求，即修改不独立时，需要先处理左区间，然后处理中间的部分，最后处理右区间。

CDQ 分治最经典的问题是三维偏序：

P3810 三维偏序

有 $n$ 个元素，第 $i$ 个元素有 $a_i$，$b_i$，$c_i$ 三个属性，设 $f(i)$ 表示满足 $a_j\leq a_i$ 且 $b_j\leq b_i$ 且 $c_j\leq c_i$ 且 $j\not= i$ 的 $j$ 的数量。

对于 $d\in[0,n)$，求 $f(i)=d$ 的数量。

首先按照 $a$ 排序。此时满足 $a_j\leq a_i$ 就是满足 $j<i$。然后考虑如何处理中间的部分。

将左右区间分别按照 $b$ 排序，然后使用类似双指针的方式遍历一遍左右区间，具体如下。

1. $b_R\geq b_L$：利用树状数组维护 $\geq c_L$ 的个数，可以发现树状数组一次的加入次数是 $O(n)$ 的。
2. $b_R<b_L$：询问树状数组 $c_R$ 处的前缀和即可。

代码中注明了一些要注意的地方。

// Problem: P3810 【模板】三维偏序（陌上花开）
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3810
// Memory Limit: 500 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
struct E{
	int a,b,c,cnt,G,id;//id for debug
}el[100001],T[100002];
inline bool cmp1(const E &a,const E &b){
	return a.a==b.a?(a.b==b.b?a.c<b.c:a.b<b.b):a.a<b.a;
}
inline bool cmp2(const E &a,const E &b){
	return a.b==b.b?a.c<b.c:a.b<b.b;
}
int n,k;
int d[100001];
int NL,NR;//two-pointers
int t[200001];//BIT
int lowbit(const int x){
	return x&-x;
}
void init(const int x){
	for(int i=x;i<=k;i++)t[i]=0;//maxc=>k;
	return;
}
void mdf(int x,int v){
	while(x<=k){//Caution! The maxnum is k. 
		t[x]+=v;//the problem is <=,when it's <,first do lowbit.
		x+=lowbit(x);//lowbit change
	}
	return;
}
int qsum(int x){
	int res=0;
	while(x>0){
		res+=t[x];
		x-=lowbit(x);
	}
	return res;//GET qian zhui he.
}
int cnt;
void solve(int l,int r){
	//cerr<<l<<" "<<r<<"\n";
	int mid=(l+r)/2;//Cut into [l,mid] and [mid+1,r]
	if(l==r)return;//Special Judge
	solve(l,mid);//Step 1: di gui to deal with the left
	solve(mid+1,r);//Step 2: di gui to deal with the right
	//Step 3: Calculate the answer which is go through mid
	//Because a's order ordered,step 2,3 can't reverse
	sort(el+l,el+mid+1,cmp2);
	sort(el+mid+1,el+r+1,cmp2);//Use b to sort,ready to use two-pointers and BIT.
	NL=l,NR=mid+1;//two-pointers
	//The Core Code
	int minnum=1e9;// ka chang
	while(NR<=r){
		while(NL<=mid&&el[NL].b<=el[NR].b)mdf(el[NL].c,el[NL].G),NL++,minnum=min(el[NL-1].c,minnum);
		el[NR].cnt+=qsum(el[NR].c);
		//if(el[NR].id==3)cerr<<qsum(el[NR].c)<<" "<<l<<" "<<r<<" test\n";
		NR++;
	}
	init(minnum);
	//End of The Core Code
	return;
}
int main(){
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	cin>>n>>k;
	for(int i=1;i<=n;i++)cin>>T[i].a>>T[i].b>>T[i].c,T[i].id=i;
	sort(T+1,T+n+1,cmp1);//Sort by a
	//now Converted a_j<=a_i to j<i
	//qu chong--- ! important
	int lst=1;
	for(int i=1;i<=n+1;i++){
		if(T[i].a!=T[lst].a||T[i].b!=T[lst].b||T[i].c!=T[lst].c){
			el[++cnt]=T[lst];
			el[cnt].G=i-lst;
			lst=i;
		}
	}
	//No li san hua's need,main working tree clean and solve()
	solve(1,cnt);
	//Output
	for(int i=1;i<=cnt;i++)d[el[i].cnt+el[i].G-1]+=el[i].G;//,cerr<<el[i].id<<" "<<el[i].cnt<<" "<<el[i].G<<"\n";
	for(int i=0;i<n;i++)cout<<d[i]<<"\n";
	return 0;
}

大多题对于 CDQ 分治的应用就是三维偏序。然后还有一个 CDQ 分治将动态问题转成静态问题的神奇东西没看懂。

例题：P3157

进行转化：

将逆序对记录到先被删除的那一个元素上，得到 $i<j,v_i>v_j,t_i\leq t_j$，特别的，不被删除的元素 $t_i=m+1$。

当然逆序对不只有这一种表达方式，还有 $i>j,v_i<v_j.t_i\leq t_j$。那么用 CDQ 分治扫两次即可。注意此时值为 $m+1$ 的 $t$ 会被算两次，要特判。

// Problem: P3157 [CQOI2011] 动态逆序对
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3157
// Memory Limit: 500 MB
// Time Limit: 1500 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define int long long
struct E{
	int id,v,t,cnt;
}el[100001];
int n,m;
//id cant be same,so no need to li san hua.
//id_i>id_j,v_i<v_j,t_i<=t_j
//cmp_id->no need.
inline bool cmp(const E &a,const E &b){
	return a.v>b.v;
}
int bu,C[100001],T[100001];
int NL,NR;
int t[100001];//m-t_i+2;
int lowbit(int x){
	return x&-x;
}
void mdf(int x,int v){
	while(x<=m+2){
		t[x]+=v;
		x+=lowbit(x);
	}
	return;
}
int qsum(int x){
	int res=0;
	while(x>0){
		res+=t[x];
		x-=lowbit(x);
	}
	return res;
}
void solve(int l,int r){
	int mid=(l+r)/2;
	if(l==r)return;
	solve(l,mid);
	solve(mid+1,r);
	sort(el+l,el+mid+1,cmp);
	sort(el+mid+1,el+r+1,cmp);
	NL=l,NR=mid+1;
	while(NR<=r){
		while(NL<=mid&&el[NL].v>=el[NR].v)mdf(m-el[NL].t+2,1),NL++;
		T[el[NR].t]+=qsum(m-el[NR].t+2);
		NR++;
	}
	for(int i=l;i<NL;i++)mdf(m-el[i].t+2,-1);
	NL=mid,NR=r;
	while(NL>=l){
		while(NR>=mid+1&&el[NL].v>=el[NR].v)mdf(m-el[NR].t+2,1),NR--;
		if(el[NL].t!=m+1)T[el[NL].t]+=qsum(m-el[NL].t+2);
		NL--;
	}
	for(int i=NR+1;i<=r;i++)mdf(m-el[i].t+2,-1);
	return;
}

signed main(){
	ios::sync_with_stdio(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>el[i].v,el[i].id=i,C[el[i].v]=i;
	for(int i=1;i<=m;i++)cin>>bu,el[C[bu]].t=i;
	for(int i=1;i<=n;i++)if(el[i].t==0)el[i].t=m+1;
	solve(1,n);
	int sum=0;
	for(int i=1;i<=m+1;i++)sum+=T[i];//,cerr<<T[i]<<"\n";
	for(int i=1;i<=m;i++){
		cout<<sum<<"\n";
		sum-=T[i];
	}
	return 0;
}

例题：P8575

首先转换偏序关系：

red_x>red_{id}\and blue_x>blue_{id}\and dfn_{id}\in[dfn_x,dfn_x+siz_x-1]

发现是一个四维偏序。

后面的部分转化为区间查询，单点修改，前面正常些就行了。

注意三维偏序题的排序都要排完整，多判相等情况。

// Problem: P8575 「DTOI-2」星之河
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P8575
// Memory Limit: 64 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
struct O{
	int red,blue,id,re,o;
}el[200001];
int n;
struct line{
	int to,link;
}E[400001];
int head[200001],tot;
void addE(int u,int v){
	E[++tot].link=head[u];
	E[tot].to=v;
	head[u]=tot;
	return;
}
int dfncnt,rk[200001];
void dfs(int now,int f){
	el[now].id=++dfncnt;
	rk[dfncnt]=now;
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==f)continue;
		dfs(E[i].to,now);
	}
	el[now].re=dfncnt;
	return;
}
int A[200001],Red[200001],Blue[200001];
inline bool cmp1(const O &a,const O &b){
	return a.red==b.red?(a.blue==b.blue?a.id>b.id:a.blue<b.blue):a.red<b.red;
}
inline bool cmp2(const O &a,const O &b){
	return a.blue<b.blue;
}
int NL,NR;
int t[300001];
int lowbit(int x){
	return x&-x;
}
void mdf(int x,int v){
	while(x<=n+1){
		t[x]+=v;
		//cerr<<x<<" "<<v<<" "<<t[x]<<"\n";
		x+=lowbit(x);
	}
	return;
}
int qsum(int x){
	int res=0;
	while(x>0){
		res+=t[x];
		x-=lowbit(x);
	}
	return res;
}
void solve(int l,int r){
	int mid=(l+r)/2;
	if(l==r)return;
	solve(l,mid);
	solve(mid+1,r);
	sort(el+l,el+mid+1,cmp2);
	sort(el+mid+1,el+r+1,cmp2);
	NL=l,NR=mid+1;
	while(NR<=r){
		while(NL<=mid&&el[NL].blue<=el[NR].blue)mdf(el[NL].id,1),NL++;
		A[el[NR].o]+=qsum(el[NR].re)-qsum(el[NR].id);
		//if(el[NR].o==3)cerr<<NR<<" "<<l<<" "<<r<<" "<<el[NR].re<<" "<<el[NR].id<<" "<<qsum(el[NR].re)-qsum(el[NR].id)<<"\n";
		NR++;
	}
	//cerr<<"test\n";
	for(int i=l;i<NL;i++)mdf(el[i].id,-1);
	return;
}
int main(){
	ios::sync_with_stdio(0);
	cin>>n;
	int x,y;
	for(int i=1;i<n;i++)cin>>x>>y,addE(x,y),addE(y,x);
	dfs(1,0);
	for(int i=1;i<=n;i++)cin>>Red[i]>>Blue[i],el[i].red=Red[i],el[i].blue=Blue[i],el[i].o=i;
	sort(Red+1,Red+n+1);
	sort(Blue+1,Blue+n+1);
	for(int i=1;i<=n;i++){
		el[i].red=lower_bound(Red+1,Red+n+1,el[i].red)-Red;
		el[i].blue=lower_bound(Blue+1,Blue+n+1,el[i].blue)-Blue;
	}
	sort(el+1,el+n+1,cmp1);
	solve(1,n);
	for(int i=1;i<=n;i++){
		if(A[i]==0)continue;
		cout<<A[i]<<"\n";
	}
	return 0;
}

应用：优化 一维dp P2487

CDQ 分治优化 dp 时需要注意转移顺序必须有序，即中序遍历，这时就要考虑排序前后数组的还原。

这道题是求二维 $LDS$，考虑记录每个点为结尾或开头的 $LDS$ 长度与方案数。由于顺序关系，需要 CDQ 分治两次。

同样的，后缀和使用倒序树状数组。此处的树状数组就是统计 $\max$ 了，记得树状数组要记录最大值和在当前最大值的方案数。

方案数可能非常非常大，使用浮点数记录。

// Problem: P2487 [SDOI2011] 拦截导弹
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2487
// Memory Limit: 500 MB
// Time Limit: 1500 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define int long long
struct E{
	int id,a,b;
}el[200001];
int n;
int t[200001];
long double kt[200001];
int A[200001],B[200001];
int lowbit(int x){
	return x&-x;
}
void reset(int x){
	while(x<=n){
		t[x]=kt[x]=0;
		x+=lowbit(x);
	}
	return;
}
void mdf(int x,int v,long double C){
	while(x<=n){
		if(t[x]<v)t[x]=v,kt[x]=C;
		else if(t[x]==v)kt[x]+=C;
		x+=lowbit(x);
	}
	return;
}
pair<int,long double> qsum(int x){
	int res=0;
	long double g=1;
	while(x>0){
		if(res<t[x])res=t[x],g=kt[x];
		else if(res==t[x])g+=kt[x];
		x-=lowbit(x);
	}
	return make_pair(res,g);
}
inline bool cmp1(const E &a,const E &b){
	return (a.a==b.a?(a.b==b.b?a.id<b.id:a.b>b.b):a.a>b.a);
}
inline bool cmp2(const E &a,const E &b){
	return a.b==b.b?a.id<b.id:a.b>b.b;
}
int NL,NR;
int f1[200001];
long double g1[200001];
void solve1(int l,int r){
	int mid=(l+r)/2;
	if(l==r)return;
	solve1(l,mid);//Step 1: Left
	//Step 2: Left---Right
	sort(el+l,el+mid+1,cmp2);
	sort(el+mid+1,el+r+1,cmp2);
	NL=l,NR=mid+1;
	while(NR<=r){
		while(NL<=mid&&el[NL].b>=el[NR].b)mdf(el[NL].id,f1[el[NL].id],g1[el[NL].id]),NL++;
		//cerr<<NL<<' '<<NR<<"\n";
		pair<int,long double> K=qsum(el[NR].id);
		if(!K.first){
			NR++;
			continue;
		}
		if(f1[el[NR].id]<K.first+1)f1[el[NR].id]=K.first+1,g1[el[NR].id]=K.second;
		else if(f1[el[NR].id]==K.first+1)g1[el[NR].id]+=K.second;
		//cerr<<el[NR].id<<" "<<f1[el[NR].id]<<" "<<g1[el[NR].id]<<"\n";
		NR++;
	}
	for(int i=l;i<NL;i++)reset(el[i].id);
	sort(el+l,el+r+1,cmp1);
	solve1(mid+1,r);
	return;
}
int f2[200001];
long double g2[200001];
void solve2(int l,int r){
	int mid=(l+r)/2;
	if(l==r)return;
	solve2(mid+1,r);
	sort(el+l,el+mid+1,cmp2);
	sort(el+mid+1,el+r+1,cmp2);
	NL=mid,NR=r;
	while(NL>=l){
		while(NR>=mid+1&&el[NL].b>=el[NR].b)mdf(n-el[NR].id+1,f2[el[NR].id],g2[el[NR].id]),NR--;
		pair<int,long double> K=qsum(n-el[NL].id+1);
		if(!K.first){
			NL--;
			continue;
		}
		if(f2[el[NL].id]<K.first+1)f2[el[NL].id]=K.first+1,g2[el[NL].id]=K.second;
		else if(f2[el[NL].id]==K.first+1)g2[el[NL].id]+=K.second;
		NL--;
	}
	for(int i=r;i>NR;i--)reset(n-el[i].id+1);
	sort(el+l,el+r+1,cmp1);
	solve2(l,mid);
	return;
}

signed main(){
	ios::sync_with_stdio(0);
	cin>>n;
	for(int i=1;i<=n;i++)cin>>A[i]>>B[i],el[i].id=i,el[i].a=A[i],el[i].b=B[i];
	sort(A+1,A+n+1);
	sort(B+1,B+n+1);
	for(int i=1;i<=n;i++){
		el[i].a=lower_bound(A+1,A+n+1,el[i].a)-A;
		el[i].b=lower_bound(B+1,B+n+1,el[i].b)-B;
	}
	sort(el+1,el+n+1,cmp1);
	for(int i=1;i<=n;i++)f1[i]++,g1[i]++,f2[i]++,g2[i]++;
	solve1(1,n);
	solve2(1,n);
	//for(int i=1;i<=n;i++)cout<<f1[i]<<" "<<g1[i]<<" "<<f2[i]<<" "<<g2[i]<<"\n";
	int len=0;
	long double sum=0;
	for(int i=1;i<=n;i++){
		len=max(f1[i]+f2[i]-1,len);
	}
	for(int i=1;i<=n;i++){
		if(len==f1[i]+f2[i]-1)sum+=g1[i]*g2[i];//,cout<<"test ";
		//cout<<i<<" "<<g1[i]<<" "<<g2[i]<<"\n";
	}
	sum/=len;
	cout<<len<<"\n";
	for(int i=1;i<=n;i++){
		if(len==f1[i]+f2[i]-1)cout<<fixed<<setprecision(5)<<1.0*g1[i]*g2[i]/sum<<" ";
		else cout<<"0.00000 ";
	}
	return 0;
}

整体二分

整体二分用于处理一些支持离线的区间查询问题，和莫队一样分为几种类型。

通常，整体二分就是把几个询问一起处理，然后把它们分到不同的子区间继续处理。

一种比较好实现的伪代码：

solve(int l,int r,int L,int R){
    //ans:in[l,r]||||asks:in[L,R]
    if l==r then for [L,R] ans[id]=l;
    Simulate mid/[l,mid];
    Count those already satisfied asks -> Q1[];
    The other -> Q2[];
    Q1[] -> Q[],Q2[] -> Q[];
    restore as when the function began except Q[];
    solve(l,mid,Q[l1,r1](Q1));
    solve(mid+1,r,Q[l2,r2](Q2));
    return;
}

要想整体二分，首先要保证数据有可二分性，然后再用数据结构优化模拟 $[l,mid]$ 的这个过程就能做到优化。

普通整体二分

例题：P3527

断环为链，用树状数组区间修改，单点询问来维护陨石数量，然后统计的时候每次超了就减去当前贡献递归向右，否则递归向左。通俗来讲，整体二分就是把一个集合分成两个集合，每个集合都有固定的值域，二分值域划分集合，最后得出答案。

// Problem: P3527 [POI2011] MET-Meteors
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3527
// Memory Limit: 512 MB
// Time Limit: 2500 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define int unsigned long long
struct qu{
	int id,l,r,v;
}Q[300002];
int n,m,q;
vector<int> C[300001];
int ne[300001];
int A[300001];
long long t[600001];
int lowbit(int x){
	return x&-x;
}
void mdf(int x,long long v){
	while(x<=m){
		t[x]+=v;
		x+=lowbit(x);
	}
	return;
}
int qsum(int x){
	int res=0;
	while(x>0){
		res+=t[x];
		x-=lowbit(x);
	}
	return res;
}
int rec[300001];
int s1[300001],s2[300001],TL,TR;

void solve(int l,int r,int L,int R){
	//cout<<l<<" "<<r<<" "<<L<<" "<<R<<"\n";
	if(l==r){
		for(int i=L;i<=R;i++)A[rec[i]]=l;
		return;
	}
	int mid=(l+r)/2;
	//Simulate [l,mid]
	for(int i=l;i<=mid;i++){
		mdf(Q[i].l,Q[i].v),mdf(Q[i].r+1,-Q[i].v);//差分
	}
	int c1=0,c2=0;
	//Counting the satisfied ones and dissatisfied ones
	for(int i=L;i<=R;i++){
		int now=0,siz=C[rec[i]].size();
		for(int j=0;j<siz;j++)now+=qsum(C[rec[i]][j]);
		if(now>=ne[rec[i]])s1[++c1]=rec[i];
		else ne[rec[i]]-=now,s2[++c2]=rec[i];
		//cout<<rec[i]<<" "<<ne[rec[i]]<<"\n";
	}
	for(int i=1;i<=c1;i++)rec[i+L-1]=s1[i];
	for(int i=1;i<=c2;i++)rec[i+c1+L-1]=s2[i];
	for(int i=l;i<=mid;i++){
		mdf(Q[i].l,-Q[i].v),mdf(Q[i].r+1,Q[i].v);//Restore
	}
	solve(l,mid,L,L+c1-1);
	solve(mid+1,r,L+c1,L+c1+c2-1);
	return;
}

signed main(){
	ios::sync_with_stdio(0);
	int te;
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		cin>>te;
		C[te].push_back(i);
		C[te].push_back(i+m);
	}
	for(int i=1;i<=n;i++){
		cin>>ne[i];
	}
	cin>>q;
	for(int i=1;i<=q;i++){
		cin>>Q[i].l>>Q[i].r>>Q[i].v;
		if(Q[i].r<Q[i].l)Q[i].r+=m;
		Q[i].id=i;
	}
	q++;
	Q[q].l=1,Q[q].r=m,Q[q].v=1e9,Q[q].id=q;
	m*=2;
	for(int i=1;i<=n;i++)rec[i]=i;
	solve(1,q,1,n);
	for(int i=1;i<=n;i++){
		if(A[i]==q)cout<<"NIE\n";
		else cout<<A[i]<<"\n";
	}
	return 0;
}

注意要用 $rec$ 数组记录当前位置处理的询问是哪个，因为为了二分答案询问是打乱了顺序的，直接用 $i$ 是不行的。

例题：P4602

鉴定为：勾矢。调了一个下午。

使用权值线段树，以单价为下标，在权值线段树上二分来找当前满足有 $L$ 升果汁时的最小花费来进行 check。

然后用类似于莫队的方式维护线段树的插入和删除，这一步非常重要，保证了时间复杂度。

中间有一些东西作者写的非常抽象，我也不想改了，调了一个下午…

// Problem: P4602 [CTSC2018] 混合果汁
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4602
// Memory Limit: 500 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define int long long
struct io{
	int d,p,l;
}J[100002];
struct qu{
	int g,l;
}Q[100002];
int rec[100002];
int n,m;
int g[600002],ll[600002];
void pushup(int now){
	ll[now]=ll[now<<1|1]+ll[now<<1];
	g[now]=g[now<<1|1]+g[now<<1];
	return;
}
void insert(int now,int l,int r,int q,int C){
	if(l==r){
		g[now]+=C*q;
		ll[now]+=C;
		return;
	}
	int mid=(l+r)/2;
	if(q<=mid)insert(now<<1,l,mid,q,C);
	else insert(now<<1|1,mid+1,r,q,C);
	pushup(now);
	return;
}
bool check(int now,int l,int r,int L,int G){
	if(l==r){
		G-=L*l;
		return G>=0;
	}
	// cerr<<ll[now];
	if(L==0)return G>=0;
	if(ll[now]<L)return 0;
	if(G<0)return 0;
	int mid=(l+r)/2;
	bool res=0;
	if(ll[now<<1]>=L)res|=check(now<<1,l,mid,L,G);
	else res|=check(now<<1|1,mid+1,r,L-ll[now<<1],G-g[now<<1]);
	return res;
}
void reset(int now,int l,int r){
	if(l==r)return ll[now]=g[now]=0,void();
	int mid=(l+r)/2;
	reset(now<<1,l,mid);
	reset(now<<1|1,mid+1,r);
	pushup(now);
	return;
}
bool cmp(const io &a,const io &b){
	return a.d>b.d;y
}
int s1[100002],s2[100002],T[100002];
int A[100002];
int MAX=100002;
int cur=0;
void solve(int l,int r,int L,int R){
	 // cerr<<l<<" "<<r<<" "<<L<<" "<<R<<"\n";
	// if(l==r){
		// for(int i=L;i<=R;i++)A[rec[i]]=l;
		// return;
	// }
	if(l>r||L>R)return;
	int mid=(l+r)/2;
	// int st=upper_bound(T+1,T+n+1,r)-T-1;
	while(J[cur+1].d>=mid&&cur<=n)cur++,insert(1,1,MAX,J[cur].p,J[cur].l);//cerr<<cur<<" "<<J[cur].d<<"\n";
	while(J[cur].d<mid&&cur>0)insert(1,1,MAX,J[cur].p,-J[cur].l),cur--;
	int c1=0,c2=0;
	for(int i=L;i<=R;i++){
		if(check(1,1,MAX,Q[rec[i]].l,Q[rec[i]].g))s2[++c2]=rec[i],A[rec[i]]=mid;
		else s1[++c1]=rec[i];
	}
	for(int i=1;i<=c1;i++)rec[i+L-1]=s1[i];
	for(int i=1;i<=c2;i++)rec[i+L+c1-1]=s2[i];
	// for(int i=n;i>=1&&J[i].d>=mid;i--)insert(1,1,MAX,J[i].p,-J[i].l);
	if(l==r)return;
	solve(l,mid-1,L,L+c1-1);
	solve(mid+1,r,L+c1,L+c1+c2-1);
	return;
}

signed main(){
	ios::sync_with_stdio(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>J[i].d>>J[i].p>>J[i].l;
	// n++;
	// J[n].d=0,J[n].p=0,J[n].l=1e9;
	for(int i=1;i<=m;i++)cin>>Q[i].g>>Q[i].l;
	for(int i=1;i<=m;i++)rec[i]=i;
	sort(J+1,J+n+1,cmp);
	for(int i=1;i<=n;i++)T[i]=J[i].d;
	solve(1,MAX,1,m);
	for(int i=1;i<=m;i++){
		if(A[i]==0)A[i]=-1;
		cout<<A[i]<<"\n";
	}
	return 0;
}

回滚整体二分

例题：P8955

整体二分的搜索树就是一颗线段树，考虑将这颗线段树分层，每次对询问排序，然后进行从左向右依次处理询问，直到到达最后一层，即 $\left\lceil\log n\right\rceil$ 层。

// Problem: P8955 「VUSC」Card Tricks
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P8955
// Memory Limit: 100 MB
// Time Limit: 3000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
namespace Fastio {
    #define IN_LEN 250000
    #define OUT_LEN 250000
    #define ll long long
//  #define Putchar putchar
//  #define Getchar getchar
    char ch; int len;

    inline char Getchar() {
        static char buf[IN_LEN], *l = buf, *r = buf;
        if (l == r) r = (l = buf) + fread(buf, 1, IN_LEN, stdin);
        return (l == r) ? EOF : *l++;
    }
    char obuf[OUT_LEN], *ooh = obuf;
    inline void Putchar(char c) {
        if (ooh == obuf + OUT_LEN) fwrite(obuf, 1, OUT_LEN, stdout), ooh = obuf;
        *ooh++ = c;
    }
    inline void flush() { fwrite(obuf, 1, ooh - obuf, stdout); }

    #undef IN_LEN
    #undef OUT_LEN
    #undef ll
    struct Reader {
        template <typename T> Reader& operator >> (T &x) {
            x = 0;
            short f = 1;
            char c = Getchar();
            while (c < '0' || c > '9') { if (c == '-') f *= -1; c = Getchar(); }
            while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + (c ^ 48), c = Getchar();
            x *= f;
            return *this;
        }
        Reader& operator >> (double &x) {
            x = 0;
            double t = 0;
            short f = 1, s = 0;
            char c = Getchar();
            while ((c < '0' || c > '9') && c != '.') { if (c == '-') f *= -1; c = Getchar(); }
            while (c >= '0' && c <= '9' && c != '.') x = x * 10 + (c ^ 48), c = Getchar();
            if (c == '.') c = Getchar();
            else { x *= f; return *this; }
            while (c >= '0' && c <= '9') t = t * 10 + (c ^ 48), s++, c = Getchar();
            while (s--) t /= 10.0;
            x = (x + t) * f;
            return *this;
        }
        Reader& operator >> (long double &x) {
            x = 0;
            long double t = 0;
            short f = 1, s = 0;
            char c = Getchar();
            while ((c < '0' || c > '9') && c != '.') { if (c == '-') f *= -1; c = Getchar(); }
            while (c >= '0' && c <= '9' && c != '.') x = x * 10 + (c ^ 48), c = Getchar();
            if (c == '.') c = Getchar();
            else { x *= f; return *this; }
            while (c >= '0' && c <= '9') t = t * 10 + (c ^ 48), s++, c = Getchar();
            while (s--) t /= 10.0;
            x = (x + t) * f;
            return *this;
        }
        Reader& operator >> (__float128 &x) {
            x = 0;
            __float128 t = 0;
            short f = 1, s = 0;
            char c = Getchar();
            while ((c < '0' || c > '9') && c != '.') { if (c == '-') f *= -1; c = Getchar(); }
            while (c >= '0' && c <= '9' && c != '.') x = x * 10 + (c ^ 48), c = Getchar();
            if (c == '.') c = Getchar();
            else { x *= f; return *this; }
            while (c >= '0' && c <= '9') t = t * 10 + (c ^ 48), s++, c = Getchar();
            while (s--) t /= 10.0;
            x = (x + t) * f;
            return *this;
        }
        Reader& operator >> (char &c) {
            c = Getchar();
            while (c == ' ' || c == '\n' || c == '\r') c = Getchar();
            return *this;
        }
        Reader& operator >> (char *str) {
            int len = 0;
            char c = Getchar();
            while (c == ' ' || c == '\n' || c == '\r') c = Getchar();
            while (c != ' ' && c != '\n' && c != '\r') str[len++] = c, c = Getchar();
            str[len] = '\0';
            return *this;
        }
        Reader& operator >> (string &str) {
            str.clear();
            char c = Getchar();
            while (c == ' ' || c == '\n' || c == '\r') c = Getchar();
            while (c != ' ' && c != '\n' && c != '\r') str.push_back(c), c = Getchar();
            return *this;
        }
        Reader() {}
    } cin;
    const char endl = '\n';
    struct Writer {

        const int Setprecision = 6;

        typedef __int128 mxdouble;
        template <typename T> Writer& operator << (T x) {
            if (x == 0) { Putchar('0'); return *this; }
            if (x < 0) Putchar('-'), x = -x;
            static short sta[40];
            short top = 0;
            while (x > 0) sta[++top] = x % 10, x /= 10;
            while (top > 0) Putchar(sta[top] + '0'), top--;
            return *this;
        }
        Writer& operator << (double x) {
            if (x < 0) Putchar('-'), x = -x;
            double _up=5;
                 for (int i = 0; i <= Setprecision; i++) _up /= 10.0;
                 x+=_up;
            mxdouble _ = x;
            x -= (double)_;
            static short sta[40];
            short top = 0;
            while (_ > 0) sta[++top] = _ % 10, _ /= 10;
            if (top == 0) Putchar('0');
            while (top > 0) Putchar(sta[top] + '0'), top--;
            Putchar('.');
            for (int i = 0; i < Setprecision; i++) x *= 10;
            _ = x;
            while (_ > 0) sta[++top] = _ % 10, _ /= 10;
            for (int i = 0; i < Setprecision - top; i++) Putchar('0');
            while (top > 0) Putchar(sta[top] + '0'), top--;
            return *this;
        }
        Writer& operator << (long double x) {
            if (x < 0) Putchar('-'), x = -x;
            long double _up=5;
            for (int i = 0; i <= Setprecision; i++) _up /= 10.0;
                 x+=_up;
            mxdouble _ = x;
            x -= (long double)_;
            static short sta[40];
            short top = 0;
            while (_ > 0) sta[++top] = _ % 10, _ /= 10;
            if (top == 0) Putchar('0');
            while (top > 0) Putchar(sta[top] + '0'), top--;
            Putchar('.');
            for (int i = 0; i < Setprecision; i++) x *= 10;
            _ = x;
            while (_ > 0) sta[++top] = _ % 10, _ /= 10;
            for (int i = 0; i < Setprecision - top; i++) Putchar('0');
            while (top > 0) Putchar(sta[top] + '0'), top--;
            return *this;
        }
        Writer& operator << (__float128 x) {
            if (x < 0) Putchar('-'), x = -x;
            __float128 _up=5;
            for (int i = 0; i <= Setprecision; i++) _up /= 10.0;
            x+=_up;
            mxdouble _ = x;
            x -= (__float128)_;
            static short sta[40];
            short top = 0;
            while (_ > 0) sta[++top] = _ % 10, _ /= 10;
            if (top == 0) Putchar('0');
            while (top > 0) Putchar(sta[top] + '0'), top--;
            Putchar('.');
            for (int i = 0; i < Setprecision; i++) x *= 10;
            _ = x;
            while (_ > 0) sta[++top] = _ % 10, _ /= 10;
            for (int i = 0; i < Setprecision - top; i++) Putchar('0');
            while (top > 0) Putchar(sta[top] + '0'), top--;
            return *this;
        }
        Writer& operator << (char c) { Putchar(c); return *this; }
        Writer& operator << (char *str) {
            int cur = 0;
            while (str[cur]) Putchar(str[cur++]);
            return *this;
        }
        Writer& operator << (const char *str) {
            int cur = 0;
            while (str[cur]) Putchar(str[cur++]);
            return *this;
        }
        Writer& operator << (string str) {
            int st = 0, ed = str.size();
            while (st < ed) Putchar(str[st++]);
            return *this;
        }
        Writer() {}
    } cout;
//    #undef Putchar
//    #undef Getchar 
}
using namespace Fastio;
#define cin Fastio::cin
#define cout Fastio::cout
#define endl Fastio::endl
int n,m,p;
struct Q{
	int l,r,id;
	inline bool operator <(const Q &a) const {
		return (r<a.r);
	}
}ans[1000001];
int A[1000001],a[1000001];
int xds[4000001],lazy[4000001];
inline void pushdown(const int now){
	lazy[now<<1]|=lazy[now],lazy[now<<1|1]|=lazy[now];
	return;
}
void bulid(const int now,const int l,const int r){
	lazy[now]=xds[now]=0;
	if(l==r){
		return xds[now]=a[l],void();
	}
	const int mid=(l+r)/2;
	bulid(now<<1,l,mid);
	bulid(now<<1|1,mid+1,r);
	return;
}
void mdf(const int now,const int l,const int r,const int sl,const int sr,const int v){
	if((v|lazy[now])==lazy[now])return;
	if(l==sl&&r==sr){
		lazy[now]|=v;
		return;
	}
	const int mid=(l+r)>>1;
	pushdown(now);
	if(sl<=mid)mdf(now<<1,l,mid,sl,min(sr,mid),v);
	if(sr>mid)mdf(now<<1|1,mid+1,r,max(sl,mid+1),sr,v);
	return;
}
int qpo(const int now,const int l,const int r,const int q){
	if(l==r)return xds[now]|lazy[now];
	const int mid=(l+r)>>1;
	pushdown(now);
	if(q<=mid)return qpo(now<<1,l,mid,q);
	else return qpo(now<<1|1,mid+1,r,q);
}
int ll[1000001],rr[1000001],vv[1000001];
signed main(){
	cin>>n>>m>>p;
	for(int i=1;i<=n;i++)cin>>a[i],ans[i].l=1,ans[i].r=m+1,ans[i].id=i;
	for(int i=1;i<=m;i++){
		cin>>ll[i]>>rr[i]>>vv[i];
	}
	int ed=log2(m)+1,cur;
	for(int i=1;i<=ed;i++){
		sort(ans+1,ans+n+1);
		cur=0;
		bulid(1,1,n);
		for(int j=1;j<=n;j++){
			//cout<<ans[j].l<<" "<<ans[j].r<<" "<<ans[j].id<<"\n";
			if(ans[j].l==ans[j].r)continue;
			#define M ((ans[j].l+ans[j].r)>>1)
			//cout<<cur<<" "<<M<<"\n";
			while(cur<M)cur++,mdf(1,1,n,ll[cur],rr[cur],vv[cur]);//,cout<<cur<<" "<<vv[cur]<<" "<<qpo(1,1,n,ans[j].id)<<" ";
			//cout<<"\n";
			//cout<<qpo(1,1,n,ans[j].id)<<"\n";
			if(qpo(1,1,n,ans[j].id)>p)ans[j].r=M;
			else ans[j].l=M+1;
		}
	}
	for(int i=1;i<=n;i++)A[ans[i].id]=ans[i].l;
	for(int i=1;i<=n;i++){
		if(A[i]==m+1)A[i]=-1;
		cout<<A[i]<<" ";
	}
	flush();
	return 0;
}

带修整体二分

由于这种整体二分的例题比较深，我们由浅入深来做这道题。

单次查询全局第 k 小

使用权值线段树上二分，时间复杂度 $O(V)$。

多次查询全局第 k 小

建出权值线段树，对所有目前询问区间正常整体二分，用权值线段树 $O(1)$ 检验。

时间复杂度 $O(q\log V+V)$。

查询区间第 k 小

模板题：P3834

不难发现由于区间不同，不可持久化权值线段树类做法不可行。考虑设计一个快速的 check 函数。

使用以数组下标为下标权值树状数组统计小于 $mid$ 的数的个数即能把 check 的总复杂度降到 $O(n\log n+q\log n)$，如果 $q$ 与 $n$ 同阶，那么总时间复杂度为 $O(n\log^2 n)$。

通过这个例子，我们可以发现其实整体二分的本质就是把所有区间的值先预处理出来（通常使用前缀和），然后猜测时把每个区间的答案猜测的一样，这样能做到该值适用于所有区间，而对值域二分分块（保证复杂度的全局优化）又将询问次数降到了 $O(n\log n)$ 次，从而降低复杂度。

AC 代码：

// Problem: P3834 【模板】可持久化线段树 2
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3834
// Memory Limit: 1 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int n,m;
struct num{
	int id,v;
}N[200001],N1[200001],N2[200001];
struct qu{
	int l,r,k,id;
}Q[200001],Q1[200001],Q2[200001];
int t[200001],ov[200001],a[200001],A[200001];
int lowbit(int x){
	return x&-x;
}
void mdf(int x,int v){
	while(x<=n){
		t[x]+=v;
		x+=lowbit(x);
	}
	return;
}
int qsum(int x){
	int res=0;
	while(x>0){
		res+=t[x];
		x-=lowbit(x);
	}
	return res;
}
void solve(int l,int r,int ll,int rr,int L,int R){
	//cerr<<l<<" "<<r<<" "<<ll<<" "<<rr<<" "<<L<<" "<<R<<"\n";
	if(l==r){
		for(int i=L;i<=R;i++)A[Q[i].id]=ov[N[ll].id];
		return;
	}
	if(L>R||l>r||ll>rr)return;
	int M=(l+r)/2;
	int CN1=0,CN2=0,CQ1=0,CQ2=0;
	for(int i=ll;i<=rr;i++){
		if(N[i].v<=M)N1[++CN1]=N[i],mdf(N[i].id,1);
		else N2[++CN2]=N[i];
	}
	//cerr<<M<<"\n";
	for(int i=L;i<=R;i++){
		int K=qsum(Q[i].r)-qsum(Q[i].l-1);
		//cerr<<Q[i].l<<" "<<Q[i].r<<" "<<K<<"\n";
		if(K>=Q[i].k)Q1[++CQ1]=Q[i];
		else Q2[++CQ2]=Q[i],Q2[CQ2].k-=K;
	}
	//cerr<<CN1<<" "<<CN2<<" "<<CQ1<<" "<<CQ2<<"\n";
	for(int i=ll;i<=rr;i++)if(N[i].v<=M)mdf(N[i].id,-1);
	for(int i=1;i<=CN1;i++)N[ll+i-1]=N1[i];
	for(int i=1;i<=CN2;i++)N[ll+CN1+i-1]=N2[i];
	for(int i=1;i<=CQ1;i++)Q[L+i-1]=Q1[i];
	for(int i=1;i<=CQ2;i++)Q[L+CQ1+i-1]=Q2[i];
	solve(l,M,ll,ll+CN1-1,L,L+CQ1-1);
	solve(M+1,r,ll+CN1,ll+CN1+CN2-1,L+CQ1,L+CQ1+CQ2-1);
	return;
}
int main(){
	ios::sync_with_stdio(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		N[i].v=a[i];
		N[i].id=i;
		ov[i]=a[i];
	}
	sort(a+1,a+n+1);
	for(int i=1;i<=n;i++){
		N[i].v=lower_bound(a+1,a+n+1,N[i].v)-a;
		//cout<<N[i].v<<"\n";
	}
	for(int i=1;i<=m;i++)cin>>Q[i].l>>Q[i].r>>Q[i].k,Q[i].id=i;
	solve(1,n,1,n,1,m);
	for(int i=1;i<=m;i++){
		cout<<A[i]<<"\n";
	}
	return 0;
}

但是这个例子中，用可持久化权值线段树能做到更优的复杂度，考虑如何优化整体二分的过程。

发现每次加入树状数组然后删掉这个步骤非常耗时，考虑将原序列排序，然后追踪分治中心，即 M，具体实现可以参照上面混合果汁的写法。

在其他题中会有较强的常数优化，在区间第 $k$ 小问题中可以将复杂度优化到类 $O(n\log n)$。

带修区间第 k 小

进入正题。

考虑进行整体二分的时候加入时间维，按顺序存储修改操作和查询操作。将修改操作分为 删除 和 加入 两种操作，这两种操作可以用树状数组维护：二分时，当删除的数在区间内，减去贡献，加入时，加入贡献，其中树状数组以原数组下标为下标即可。

总的来说非常巧妙，画一个整体二分搜索树应该就可以理解了。

例题：P2617

// Problem: P2617 Dynamic Rankings
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2617
// Memory Limit: 512 MB
// Time Limit: 3000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
struct o{
	int x,y,k,id;
	bool ty;
	//ty==1:Query [x,y] kth
	//ty==0:Change t[x]<-add->y or t[x]-del-y k-in-{-1,1}
	void init(int _x,int _y,int _k,bool _ty,int _id=0){
		x=_x,y=_y,k=_k,ty=_ty,id=_id;
		return;
	}
}O[500005];
int cnt;
int n,m;
int a[200001],A[200001];
char c;
int t;
int tr[500005];
int lowbit(int x){
	return x&-x;
}
void mdf(int x,int v){
	while(x<=n){
		tr[x]+=v;
		x+=lowbit(x);
	}
	return;
}
int qsum(int x){
	int res=0;
	while(x>0){
		res+=tr[x];
		x-=lowbit(x);
	}
	return res;
}
o O1[500005],O2[500005];

void solve(int l,int r,int L,int R){
	//cerr<<l<<" "<<r<<" "<<L<<" "<<R<<"\n";
	int M=(l+r)/2;
	if(l>r||L>R)return;
	if(l==r){
		for(int i=L;i<=R;i++)if(O[i].ty)A[O[i].id]=l;//cout<<l<<"\n";
		return;
	}
	int ocnt1=0,ocnt2=0;
	for(int i=L;i<=R;i++){
		if(O[i].ty==1){
			int K=qsum(O[i].y)-qsum(O[i].x-1);
			//cerr<<O[i].x<<" "<<O[i].y<<" "<<O[i].k<<" "<<O[i].id<<" "<<K<<" test\n";
			if(K>=O[i].k)O1[++ocnt1]=O[i];
			else O[i].k-=K,O2[++ocnt2]=O[i];
		}
		else{
			if(O[i].y<=M)mdf(O[i].x,O[i].k),O1[++ocnt1]=O[i];
			else O2[++ocnt2]=O[i];
		}
	}
	for(int i=1;i<=ocnt1;i++)if(O1[i].ty==0)mdf(O1[i].x,-O1[i].k);
	for(int i=1;i<=ocnt1;i++)O[i+L-1]=O1[i];//,cerr<<O1[i].id<<" 1\n";
	for(int i=1;i<=ocnt2;i++)O[i+L+ocnt1-1]=O2[i];//,cerr<<O2[i].id<<" 2\n";
	solve(l,M,L,L+ocnt1-1);
	solve(M+1,r,L+ocnt1,L+ocnt1+ocnt2-1);
	return;
}

int main(){
	ios::sync_with_stdio(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>t;
		a[i]=t;
		O[++cnt].init(i,t,1,0);
	}
	int X=0,Y=0,Z=0,Qid=0;
	for(int i=1;i<=m;i++){
		cin>>c;
		cin>>X>>Y;
		if(c=='Q'){
			cin>>Z;
			O[++cnt].init(X,Y,Z,1,++Qid);
		}
		else{
			O[++cnt].init(X,a[X],-1,0);
			a[X]=Y;
			O[++cnt].init(X,a[X],1,0);
		}
	}
	solve(0,1e9,1,cnt);
	for(int i=1;i<=Qid;i++)cout<<A[i]<<"\n";
	
	return 0;
}

一些题

P4849

不难发现是一个四维偏序的 dp。

2023/11/14 小声 bb：考虑 NOIP 应该不会考这种东西，于是先鸽，去做倍增和图论了。

2023/11/21：回来了。

前置知识是嵌套式 CDQ 分治，即 CDQ 套 CDQ 这种。

考虑树状数组的方法的本质：使用分割的方式把区间信息分为两半，此时保证有序，可以直接进行第二维的排序。

以三维偏序为例，在进行 CDQ 嵌套的过程中，我们将第一维标记下来，左区间为 $0$，右区间为 $1$。不难发现，能贡献的点对只可能是 $((0,b_1,c_1),(1,b_2,c_2))$。那么直接对第二维进行排序（类似于树状数组做法的排序），将第二维的左右区间分开，使得能贡献的点对变为 $((0,L,c_1),(1,R,c_2))$。那么只需要对左右区间的第三维排序即可。这个时候只需要保证左区间标记为 $0$ 的进行统计，右区间标记为 $1$ 的进行询问。

三维偏序的参考代码：

// Problem: P3810 銆愭ā鏉裤€戜笁缁村亸搴忥紙闄屼笂鑺卞紑锛?
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3810
// Memory Limit: 500 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
struct qu{
	int a,b,c,cnt,ans;
	bool flg;
	bool operator != (const qu &p) const {
		return (p.a!=a||p.b!=b||p.c!=c);
	}
}Q[200005],T[200005],tmp[200005];
int po;
bool cmp1(const qu &a,const qu &b){
	return (a.a==b.a?(a.b==b.b?a.c<b.c:a.b<b.b):a.a<b.a);
}
bool cmp2(const qu &a,const qu &b){
	return (a.b==b.b?a.c<b.c:a.b<b.b);
}
bool cmp3(const qu &a,const qu &b){
	return a.c<b.c;
}
int n,m;
int A[200005];
void cdq2d(int l,int r){
//	cerr<<l<<" "<<r<<"\n";
	if(l==r)return;
	int mid=(l+r)/2;
	cdq2d(l,mid);
	cdq2d(mid+1,r);
	// sort(Q+l,Q+mid+1,cmp3);
	// sort(Q+mid+1,Q+r+1,cmp3);
	int C=0;
	po=l;
	int i,j;
	for(i=l,j=mid+1;j<=r;j++){
		while(Q[i].c<=Q[j].c&&i<=mid){
			i++;
			if(Q[i-1].flg==0)C+=Q[i-1].cnt;
			tmp[po++]=Q[i-1];
		}
		if(Q[j].flg)Q[j].ans+=C;
		// cerr<<l<<" "<<r<<" "<<Q[j].a<<" "<<Q[j].b<<" "<<Q[j].c<<" "<<Q[j].ans<<" "<<Q[i].flg<<"\n";
		tmp[po++]=Q[j];
	}
	while(i<=mid)i++,tmp[po++]=Q[i-1];
	for(i=l;i<=r;i++)Q[i]=tmp[i];
	return;
}
void cdq1d(int l,int r){
	if(l==r)return;
	int mid=(l+r)/2;
	cdq1d(l,mid);
	cdq1d(mid+1,r);
	sort(Q+l,Q+r+1,cmp1);
	for(int i=l;i<=mid;i++){
		Q[i].flg=0;
	}
	for(int i=mid+1;i<=r;i++){
		Q[i].flg=1;
	}
	stable_sort(Q+l,Q+r+1,cmp2);
	// cerr<<l<<" "<<r<<"\n";
	cdq2d(l,r);
	return;
}
int main(){
	ios::sync_with_stdio(0);
	cin>>n>>m;
	int pp=n;
	for(int i=1;i<=n;i++){
		cin>>T[i].a>>T[i].b>>T[i].c;
	}
	sort(T+1,T+n+1,cmp1);
	int qcnt=0;
	for(int i=1,now=1;i<=n+1;i++){
		if(T[i]!=T[now])Q[++qcnt]=T[now],Q[qcnt].cnt=i-now,now=i;
	}
	n=qcnt;
	cdq1d(1,n);
	for(int i=1;i<=n;i++)Q[i].ans+=Q[i].cnt-1,A[Q[i].ans]+=Q[i].cnt;//,cout<<Q[i].a<<" "<<Q[i].b<<" "<<Q[i].c<<" "<<Q[i].ans<<"\n";
	for(int i=0;i<pp;i++)cout<<A[i]<<"\n";
	return 0;
}

下面就是四维偏序 + 1D/1D 动态规划的 dp 的嵌套 CDQ 的题了。

使用 cdq+cdq+BIT 自认为最好写：

// Problem: P4849 寻找宝藏
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4849
// Memory Limit: 125 MB
// Time Limit: 3000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define int long long
struct qu{
	int a,b,c,d,ans,cas,val,cnt;
	bool flg;
	bool operator != (const qu &p) const {
		return (a!=p.a||b!=p.b||c!=p.c||d!=p.d);
	}
}Q[80005],T[80005],tmp[80005];
int t[80005],c[80005];
int n,m;
int lowbit(int x){
	return x&-x;
}
void clear(int x){
	while(x<=80000){
		t[x]=0;
		c[x]=0;
		x+=lowbit(x);
	}
	return;
}
void mdf(int x,int v,int C){
	while(x<=80000){
		if(t[x]<v)c[x]=C,t[x]=v;
		else if(t[x]==v)c[x]+=C;
		x+=lowbit(x);
	}
	return;
}
pair<int,int> q(int x){
	int res=0,cc=0;
	while(x>0){
		if(t[x]>res)cc=c[x],res=t[x];
		else if(t[x]==res)cc+=c[x];
		x-=lowbit(x);
	}
	return make_pair(res,cc);
}
bool cmp1(const qu &a,const qu &b){
	return a.a==b.a?(a.b==b.b?(a.c==b.c?a.d<b.d:a.c<b.c):a.b<b.b):a.a<b.a;
}
bool cmp2(const qu &a,const qu &b){
	return a.b==b.b?(a.c==b.c?a.d<b.d:a.c<b.c):a.b<b.b;
}
bool cmp3(const qu &a,const qu &b){
	return a.c==b.c?a.d<b.d:a.c<b.c;
}
int D[80001];
void cdq2d(int l,int r){
	if(l==r)return;
	int mid=(l+r)/2;
	cdq2d(l,mid);
	stable_sort(Q+l,Q+r+1,cmp2);
	stable_sort(Q+l,Q+mid+1,cmp3);
	stable_sort(Q+mid+1,Q+r+1,cmp3);
	int i,j;
	for(i=l,j=mid+1;j<=r;j++){
		while(i<=mid&&Q[i].c<=Q[j].c){
			i++;
			if(Q[i-1].flg==0)mdf(Q[i-1].d,Q[i-1].ans,Q[i-1].cas);
		}
		if(Q[j].flg){
			auto nowans=q(Q[j].d);
			if(Q[j].ans<nowans.first+Q[j].val)Q[j].ans=nowans.first+Q[j].val,Q[j].cas=nowans.second;
			else if(Q[j].ans==nowans.first+Q[j].val)Q[j].cas+=nowans.second;
			// cerr<<nowans.first<<" "<<Q[j].ans<<" "<<Q[j].cas<<" "<<Q[j].a<<" "<<Q[j].b<<" "<<Q[j].c<<" "<<Q[j].d<<"\n";
		}
	}
	for(i--;i>=l;i--)if(Q[i].flg==0)clear(Q[i].d);
	stable_sort(Q+mid+1,Q+r+1,cmp2);
	cdq2d(mid+1,r);
	return;
}
void cdq1d(int l,int r){
	if(l==r)return;
	int mid=(l+r)/2;
	cdq1d(l,mid);
	sort(Q+l,Q+r+1,cmp1);
	for(int i=l;i<=mid;i++)Q[i].flg=0;
	for(int i=mid+1;i<=r;i++)Q[i].flg=1;
	stable_sort(Q+l,Q+r+1,cmp2);
	cdq2d(l,r);
	stable_sort(Q+l,Q+r+1,cmp1);
	cdq1d(mid+1,r);
	return;
}
signed main(){
	ios::sync_with_stdio(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>T[i].a>>T[i].b>>T[i].c>>T[i].d>>T[i].val,D[i]=T[i].d;
	sort(D+1,D+n+1);
	for(int i=1;i<=n;i++)T[i].d=lower_bound(D+1,D+n+1,T[i].d)-D;
	stable_sort(T+1,T+n+1,cmp1);
	int qcnt=0;
	for(int i=1,now=1,nowsum=0;i<=n+1;i++){
		if(T[i]!=T[now])Q[++qcnt]=T[now],Q[qcnt].cnt=i-now,Q[qcnt].val=nowsum,Q[qcnt].ans=nowsum,Q[qcnt].cas=1,nowsum=0,now=i;
		nowsum+=T[i].val;
	}
	n=qcnt;
	cdq1d(1,n);
	int maxx=0,fangan=0;
	for(int i=1;i<=qcnt;i++){
		if(Q[i].ans>maxx)maxx=Q[i].ans,fangan=Q[i].cas;
		else if(Q[i].ans==maxx)fangan+=Q[i].cas;
	}
	cout<<maxx<<"\n"<<fangan%998244353<<"\n";
	return 0;
}

记得要多用 stable_sort，虽然我也不知道为什么。

P2717/P7868

其实对于每个数都减 $k$ 之后，就是个前缀和的二维偏序：满足 pre_i\geq pre_j\and id_i<id_j。

使用 CDQ 分治或者树状数组二维数点即可。

// Problem: P2717 寒假作业
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2717
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
#define int long long
using namespace std;
int a[100001],v[100001];
int n,k,ans;
void cdq(int l,int r){
	if(l==r)return;
	int mid=(l+r)/2;
	cdq(l,mid);
	cdq(mid+1,r);
	int i,j,C=0,po=l;
	for(i=l,j=mid+1;j<=r;j++){
		while(a[i]<=a[j]&&i<=mid){
			i++;
			C++;
			v[po++]=a[i-1];
		}
		ans+=C,v[po++]=a[j];
	}
	while(i<=mid)v[po++]=a[i],i++;
	for(i=l;i<=r;i++)a[i]=v[i];
	return;
}
signed main(){
	ios::sync_with_stdio(0);
	cin>>n>>k;
	for(int i=1;i<=n;i++)cin>>a[i],a[i]-=k,a[i]+=a[i-1];
	cdq(0,n);
	cout<<ans;
	return 0;
}

P7424

整体二分练习题。

显然，答案具有可二分性，那么直接整体二分答案，模拟 $[l,mid]$ 的射弹过程，合法的区间放左边，不合法的区间放右边且减去当前答案即可。注意要检验当前答案合法性，不然当有木板没有被打碎时会多计算。

// Problem: P7424 [THUPC2017] 天天爱射击
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P7424
// Memory Limit: 500 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
struct wood{
	int l,r,k;
}Q[200001],Q1[200001],Q2[200005];
int n,m,shot[200001];
int t[200005];
int lowbit(int x){
	return x&-x;
}
void mdf(int x,int v){
	while(x<=200000){
		t[x]+=v;
		x+=lowbit(x);
	}
	return;
}
int q(int x){
	int res=0;
	while(x>0){
		res+=t[x];
		x-=lowbit(x);
	}
	return res;
}
int ans[200001];
void solve(int l,int r,int L,int R){
	// cerr<<l<<" "<<r<<" "<<L<<" "<<R<<"\n";
	if(l==r){
		mdf(shot[l],1);
		for(int i=L;i<=R;i++){
			int chk=q(Q[i].r)-q(Q[i].l-1);
			if(chk>=Q[i].k)ans[l]++;
	//		cout<<Q[i].l<<" "<<Q[i].r<<" "<<Q[i].k<<" "<<chk<<"\n";
		}
		mdf(shot[l],-1);
		return;
	}
	if(l>r)return;
	int mid=(l+r)/2;
	int po1=0,po2=0;
	for(int i=l;i<=mid;i++)mdf(shot[i],1);
	for(int i=L;i<=R;i++){
		int chk=q(Q[i].r)-q(Q[i].l-1);
		if(chk>=Q[i].k)Q1[++po1]=Q[i];
		else Q2[++po2]=Q[i],Q2[po2].k-=chk;//,cout<<Q[i].l<<" "<<Q[i].r<<" "<<chk<<"\n";
	}
	for(int i=L;i<=L+po1-1;i++)Q[i]=Q1[i-L+1];
	for(int i=L+po1;i<=L+po2+po1-1;i++)Q[i]=Q2[i-L-po1+1];
	for(int i=l;i<=mid;i++)mdf(shot[i],-1);
	solve(l,mid,L,L+po1-1);
	solve(mid+1,r,L+po1,L+po1+po2-1);
	return; 
}

int main(){
	ios::sync_with_stdio(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>Q[i].l>>Q[i].r>>Q[i].k;
	for(int i=1;i<=m;i++)cin>>shot[i];
	solve(1,m,1,n);
	for(int i=1;i<=m;i++)cout<<ans[i]<<"\n";
	return 0;
}

P3380

属于是整体二分毕业题了。

这里如果使用两次整体二分的算法，那么就可以用树状数组，就是将前驱后继都转化成排名为 $\operatorname{rk}(num)$ 的形式，第一遍求出 $\operatorname{rk}(num)$，第二次再去求第 $k$ 大就行了。

而存在只使用一次整体二分的算法（我写的这个），但是只能使用线段树，于是由于常数原因，是跑不过上面的算法的。

下面就来一个操作一个操作的讲解。

首先，这种整体二分是操作序列上的值域整体二分。即脱离原数列的整体二分。

• 求 $k$ 的排名。考虑先比较 $k$ 和当前值域分治中心的大小，如果 $k$ 更大，那么可以直接在答案中加入当前值域区间 $[l,mid]$ 的贡献，然后放在右区间继续求排名。注意排名的答案有初始值 $1$。
• 求第 $k$ 小。正常求就行了，见带修区间第 $k$ 小。
• 求前驱。考虑当 $mid< k$ 时（即 $k$ 在右区间时），取左区间的最大值与答案作 $\max$。
• 求后继。与前驱差不多，当 $mid\geq k$ 时（即 $k$ 在左区间时），取右区间的最小值作 $\min$。

这个时候，线段树和修改操作的实现就有些不同了。首先确定线段树要维护区间和，区间最大最小值。

修改的时候对于 $k>mid$ 的数不加，只修改最小值；而对于 $k\leq mid$ 的数要加，只修改最大值。修改最大最小值时，利用线段树上元素只可能为 $0$ 或者 $1$，所以需要注意的是当该元素修改后为 $1$ 时将最大最小值更新为当前的数，否则最小值更新为 $+\infty\ (2147483647\to \infty)$，最大值更新为 $-\infty$。

可能讲的不太清楚。可以看看代码理解一下。

由于这份代码没有调几下就过了，我都不敢相信，所以可能有些谬误，欢迎指出。

// Problem: P3380 【模板】二逼平衡树（树套树）
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3380
// Memory Limit: 512 MB
// Time Limit: 2000 ms
// Start coding at 2023-11-30 14:48:41
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int n,m,x;
struct qu{
	// int ;//0->modify(c=1,-1,k in 0,1e8),1->kth,2->rk(k),3->pre,4->suf
	int ty,C,l,r,k,id;
}Q[200001],Q1[200001],Q2[200001];
int ans[200001];
int xdsmax[400001],xdsmin[400001],xdssum[400001];
void pushup(int now){
	xdsmax[now]=max(xdsmax[now<<1],xdsmax[now<<1|1]);
	xdsmin[now]=min(xdsmin[now<<1],xdsmin[now<<1|1]);
	xdssum[now]=xdssum[now<<1]+xdssum[now<<1|1];
	return;
}
void mdf(int now,int l,int r,int q,int num,int v,bool T){
	if(l==r){
		if(T){
			if(v==1)xdsmin[now]=num;
			else xdsmin[now]=2147483647;
		}
		else{
			xdssum[now]+=v;
			if(xdssum[now])xdsmax[now]=num;
			else xdsmax[now]=-2147483647;
		}
		return ;
	}
	int mid=(l+r)/2;
	if(q<=mid)mdf(now<<1,l,mid,q,num,v,T);
	else mdf(now<<1|1,mid+1,r,q,num,v,T);
	pushup(now);
	return;
}
void clear(int now,int l,int r,int q){
	xdsmin[now]=2147483647;
	xdsmax[now]=-2147483647;
	xdssum[now]=0;
	if(l==r)return;
	int mid=(l+r)/2;
	if(q<=mid)clear(now<<1,l,mid,q);
	else clear(now<<1|1,mid+1,r,q);
	return;
}
int qsum(int now,int l,int r,int sl,int sr){
	if(l==sl&&r==sr)return xdssum[now];
	int mid=(l+r)/2,res=0;
	if(sl<=mid)res+=qsum(now<<1,l,mid,sl,min(sr,mid));
	if(sr>mid)res+=qsum(now<<1|1,mid+1,r,max(sl,mid+1),sr);
	pushup(now);
	return res;
}
int qmax(int now,int l,int r,int sl,int sr){
	if(l==sl&&r==sr)return xdsmax[now];
	int mid=(l+r)/2,res=-2147483647;
	if(sl<=mid)res=max(res,qmax(now<<1,l,mid,sl,min(sr,mid)));
	if(sr>mid)res=max(res,qmax(now<<1|1,mid+1,r,max(sl,mid+1),sr));
	pushup(now);
	return res;
}
int qmin(int now,int l,int r,int sl,int sr){
	if(l==sl&&r==sr)return xdsmin[now];
	int mid=(l+r)/2,res=2147483647;
	if(sl<=mid)res=min(res,qmin(now<<1,l,mid,sl,min(mid,sr)));
	if(sr>mid)res=min(res,qmin(now<<1|1,mid+1,r,max(mid+1,sl),sr));
	pushup(now);
	return res;
}
int qcnt;
void solve(int l,int r,int L,int R){
	if(l>r||L>R)return;
	if(l==r){
		for(int i=L;i<=R;i++){
			if(Q[i].ty==1)ans[Q[i].id]=l;
		}
		return;
	}
	int M=(l+r)/2,cnt1=0,cnt2=0;
	for(int i=L;i<=R;i++){
		if(Q[i].ty==0){
			mdf(1,1,n,Q[i].l,Q[i].k,Q[i].C,Q[i].k>M);
			if(Q[i].k<=M)Q1[++cnt1]=Q[i];
			else Q2[++cnt2]=Q[i];
		}else if(Q[i].ty==1){
			int st=qsum(1,1,n,Q[i].l,Q[i].r);
			// cerr<<std<<"\n";
			if(st>=Q[i].k)Q1[++cnt1]=Q[i];
			else Q[i].k-=st,Q2[++cnt2]=Q[i];
		}else if(Q[i].ty==2){
			if(Q[i].k<=M)Q1[++cnt1]=Q[i];
			else ans[Q[i].id]+=qsum(1,1,n,Q[i].l,Q[i].r),Q2[++cnt2]=Q[i];
		}else if(Q[i].ty==3){
			if(Q[i].k>M){
				Q2[++cnt2]=Q[i];
				ans[Q[i].id]=max(ans[Q[i].id],qmax(1,1,n,Q[i].l,Q[i].r));
			}
			else Q1[++cnt1]=Q[i];
		}else{
			if(Q[i].k<=M){
				Q1[++cnt1]=Q[i];
				ans[Q[i].id]=min(ans[Q[i].id],qmin(1,1,n,Q[i].l,Q[i].r));
			}
			else Q2[++cnt2]=Q[i];
		}
	}
	for(int i=L;i<=R;i++)if(Q[i].ty==0)clear(1,1,n,Q[i].l);
	for(int i=1;i<=cnt1;i++)Q[i+L-1]=Q1[i];
	for(int i=1;i<=cnt2;i++)Q[i+L+cnt1-1]=Q2[i];
	solve(l,M,L,L+cnt1-1);
	solve(M+1,r,L+cnt1,L+cnt1+cnt2-1);
	return;
}
int op,l,r,pos,a[50004],ii;
int main(){
	ios::sync_with_stdio(0);
	cin>>n>>m;
	for(int i=1;i<=n*8;i++)xdsmin[i]=2147483647,xdsmax[i]=-2147483647;
	for(int i=1;i<=n;i++){
		cin>>x;
		Q[++qcnt]={0,1,i,0,x,0};
		a[i]=x;
	}
	int k;
	for(int i=1;i<=m;i++){
		cin>>op;
		if(op==1){
			cin>>l>>r>>k;
			Q[++qcnt]={2,0,l,r,k,++ii};
			ans[ii]=1;
		}else if(op==2){
			cin>>l>>r>>k;
			Q[++qcnt]={1,0,l,r,k,++ii};
		}else if(op==3){
			cin>>pos>>k;
			Q[++qcnt]={0,-1,pos,0,a[pos],0};
			a[pos]=k;
			Q[++qcnt]={0,1,pos,0,a[pos],0};
		}else if(op==4){
			cin>>l>>r>>k;
			Q[++qcnt]={3,0,l,r,k,++ii};
			ans[ii]=-2147483647;
		}else{
			cin>>l>>r>>k;
			Q[++qcnt]={4,0,l,r,k,++ii};
			ans[ii]=2147483647;
		}
	}
	solve(0,1e8,1,qcnt);
	for(int i=1;i<=ii;i++)cout<<ans[i]<<"\n";
	return 0;
}

前缀和与差分

倍增

糊里糊涂的就先写倍增了。

例题：P7167

用单调栈维护该圆盘会流到下面哪个圆盘里，发现是一个倒着的关系树。

考虑类似于求 LCA 的倍增，对于每个点维护第 $2^i$ 的祖先和要跳到第 $2^i$ 祖先需要的水量，然后像求 LCA 那样倍增就行了。

当然第二个可以用树上前缀和做。

// Problem: P7167 [eJOI2020 Day1] Fountain
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P7167
// Memory Limit: 512 MB
// Time Limit: 1500 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define int long long
struct line{
	int to,link;
}E[400001];
int head[100005],tot;
void addE(int u,int v){
	E[++tot].link=head[u];
	E[tot].to=v;
	head[u]=tot;
	return;
}
int V[100005][21],fa[100005][21];
void dfs(int now,int f){
	fa[now][0]=f;
	for(int i=0;i<20;)i++,fa[now][i]=fa[fa[now][i-1]][i-1],V[now][i]=V[now][i-1]+V[fa[now][i-1]][i-1];
	for(int i=head[now];i;i=E[i].link){
		if(E[i].to==f)continue;
		dfs(E[i].to,now);
	}
	//cout<<fa[now][0]<<" "<<V[now][0]<<" "<<fa[now][1]<<" "<<V[now][1]<<" "<<V[now][2]<<"\n";
	return;
}
int Q(int now,int v){
	//cerr<<v<<"\n";
	for(int i=20;i>=0;i--){
	//	if(V[now][i]==0)continue;
		//cerr<<V[now][i]<<" "<<now<<" -> ";
		if(v>V[now][i])v-=V[now][i],now=fa[now][i];
		//cerr<<now<<"\n";
		if(now==0||now==1e5+1)return 0;
	}
	//cerr<<"\n";
	return now;
}
int n,m;
int d[100001];
stack<int> s;
signed main(){
	ios::sync_with_stdio(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>d[i]>>V[i][0];
	}
	s.push(1);
	for(int i=2;i<=n;i++){
		while(!s.empty()&&d[s.top()]<d[i])addE(s.top(),i),addE(i,s.top()),s.pop();
		s.push(i);
	}
	while(!s.empty()){
		addE(1e5+1,s.top());
		addE(s.top(),1e5+1);
		s.pop();
	}
	dfs(1e5+1,0);
	//cerr<<fa[260][0]<<" "<<fa[260][1];
	int x,y;
	while(m--){
		cin>>x>>y;
		cout<<Q(x,y)<<"\n";
	}
	return 0;
}

例题：P4155

考虑将问题转化，就是给定一些区间，对于每个区间，求如果强制选定该区间时，覆盖整个环的最小区间数。

首先断环为链，然后按左端点排序，由于每个区间不包含，所以左右端点都满足单调性，可以用双指针求出对于每一个区间，落在该区间的最右边的左端点，这样就求出了这个区间可以接着的最右边的区间，也就是最优的区间。然后倍增求出下第 $2^i$ 个区间，只需要满足 $l_{now}\leq r_{end}-m$ 就合法。最后别忘了加上起始区间和终点区间。

注意断环为链时，跨过 $n\to 1$ 的区间的那些区间也要加入两次，但是其实可以只用加原来的区间和 $[l+m,m\times 2]$ 这个区间，因为在答案内的 $l$ 最多就是 $m$，也就是右端点最大就是 $m\times 2$，而跨过 $n\to1$ 的那些区间如果按 $[l+m,r+m\times 2]$ 加入，右端点一定大于 $m\times 2$，那么就可以加入右端点为 $m\times 2$ 的区间，防止爆 int。

// Problem: P4155 [SCOI2015] 国旗计划
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4155
// Memory Limit: 250 MB
// Time Limit: 1500 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int nxt[400005][23];
int n,m;
struct S{
	pair<int,int> p;
	int id;
	bool operator < (const S &a) const {
		return p<a.p;
	}
}seg[400005];
int ans[200005];
#define l first
#define r second
signed main(){
	ios::sync_with_stdio(0);
	cin>>n>>m;
	int x,y;
	int cnt=0;
	for(int i=1;i<=n;i++){
		cin>>x>>y;
		if(y<x){
			y+=m;
			seg[++cnt]={make_pair(x,y),i};
			seg[++cnt]={make_pair(x+m,2*m),200001};
		}
		else{
			seg[++cnt]={make_pair(x,y),i};
			seg[++cnt]={make_pair(x+m,y+m),200001};
		}
	}
	sort(seg+1,seg+cnt+1);
	//for(int i=1;i<=cnt;i++){
	//	cerr<<i<<" "<<seg[i].p.l<<" "<<seg[i].p.r<<" "<<seg[i].id<<"\n";
	//}
	for(int i=1,j=1;i<=cnt;i++){
		while(j<cnt&&seg[j+1].p.l<=seg[i].p.r)j++;
		nxt[i][0]=j;
		//cout<<seg[i].id<<" "<<i<<" "<<j<<"\n";
	}
	seg[0]={make_pair(1,INT_MAX),200001};
	for(int i=1;i<=20;i++){
		for(int j=1;j<=cnt;j++){
			nxt[j][i]=nxt[nxt[j][i-1]][i-1];
		}
	}
	for(int i=1;i<=cnt;i++){
		// int L=seg[i].p.l,R=seg[i].p.r;
		int A=i,c=0;
		for(int j=20;j>=0;j--){
			if(seg[nxt[A][j]].p.r-seg[i].p.l<m)A=nxt[A][j],c+=(1<<j);
		}
		ans[seg[i].id]=c+2;
	}
	for(int i=1;i<=n;i++)cout<<ans[i]<<" ";
	return 0;
}