线段树&平衡树

FHQ-Treap

其实就是一个通过笛卡尔树的微妙性质实现的平衡树。

不谈复杂度，只需要分析分裂合并都该如何实现就行了。

  • 分裂：

就是将一棵树分裂成一个权值小于等于 aa 和大于 aa 两部分。分裂途中遍历到当前节点，如果该节点权值小于等于 aa，那么将左子树全部合并到左边的 Treap，反之亦然。

1
2
3
4
5
6
7
8
9
void split(int now,int k,int &x,int &y){//返回x,y：是分裂出两棵 Treap 的根,now初始值为rt
    if(!now)x=y=0;
    else{
        if(val[now]<=k)x=now,split(ch[now][1],k,ch[now][1],y);
        else y=now,split(ch[now][0],k,x,ch[now][0]);
        pushup(now);
    }
    return;
}
  • 合并：

这个操作就是对于根为 xx 和 yy 的两棵树合并起来，其中要保证 xx 树的权值比 yy 小。合并的时候不难发现为了保持平衡，我们需要用堆的性质比较当前的两个节点。

如果当前 xx 树的节点比 yy 树的节点的优先值更小，那么当前 xx 树的节点就是 yy 树目前根的父亲（右儿子），反之亦然。

1
2
3
4
5
6
7
8
9
10
11
12
13
int merge(int x,int y){//返回值是根结点编号
    if(!x||!y)return x+y;
    else if(pri[x]>pri[y]){
        ch[x][1]=merge(ch[x][1],y);
        pushup(x);
        return x;
    }
    else{
        ch[y][0]=merge(x,ch[y][0]);
        pushup(y);
        return y;
    }
}

区间操作：类似于文艺平衡树的题需要使用。

这个时候就要用到 Treap 的第二种分裂方式了：按前 kk 个分裂，即前 kk 个分到一个 Treap 中，另外的分到另一个 Treap 中。

和权值分裂类似，就是如果第 kk 大在左子树中，那么将这个节点放到分裂出来后右边的 Treap 遍历左儿子，否则放到左边的 Treap 然后遍历右儿子。

文艺平衡树要实现的区间翻转操作非常好，就是维护左右儿子翻转的 tag 就行了。按 siz 分裂，按堆合并就行了，但是要当心 00 节点的 siz 要为 00。注意要把区间完全分裂出来进行操作，即先 split(rt,r,x,y);，再 split(x,l-1,w,z);。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
// Problem: P3391 【模板】文艺平衡树
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3391
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int n,m,x,y;
const int maxn=1e5+5;
int siz[maxn],ch[maxn][2],pri[maxn],tag[maxn];
int cnt,rt;
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
int addP(int v){
	siz[++cnt]=1;
	pri[cnt]=rnd();
	return cnt;
}
void pushup(int now){
	siz[now]=siz[ch[now][0]]+siz[ch[now][1]]+1;
	return;
}
void pushdown(int now){
	if(tag[now]){
		tag[now]=0;
		swap(ch[now][0],ch[now][1]);
		tag[ch[now][0]]^=1;
		tag[ch[now][1]]^=1;
	}
	return;
}
void split(int now,int k,int &x,int &y){
	if(!now)return x=y=0,void();
	else{
		pushdown(now);
		if(k<=siz[ch[now][0]])y=now,split(ch[now][0],k,x,ch[now][0]);
		else x=now,split(ch[now][1],k-siz[ch[now][0]]-1,ch[now][1],y);
	}
	pushup(now);
	return;
}
int merge(int x,int y){
	if(!x||!y)return x+y;
	else{
		if(pri[x]>pri[y]){
			pushdown(x);
			ch[x][1]=merge(ch[x][1],y);
			pushup(x);
			return x;
		}
		else{
			pushdown(y);
			ch[y][0]=merge(x,ch[y][0]);
			pushup(y);
			return y;
		}
	}
}
void print(int now){
	if(!now)return;
	pushdown(now);
	print(ch[now][0]);
	cout<<now<<" ";
	print(ch[now][1]);
	pushup(now);
	return;
}
int main(){
	ios::sync_with_stdio(0);
	int n,m,x,y;
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		rt=merge(rt,addP(i));
	}
	int l,r,w,z;
	while(m--){
		cin>>l>>r;
		split(rt,r,x,y);
		split(x,l-1,w,z);
		tag[z]^=1;
		rt=merge(merge(w,z),y);
	//	print(rt);
		//cout<<"\n"<<rt<<" "<<w<<" "<<z<<" "<<siz[rt]<<" "<<siz[0]<<"\n";
	}
	print(rt);
	return 0;
}

Trick 1: 复杂信息合并

直接拆标记就行了。

例题：P7706

题意：有两个序列 AiA_i 和 BiB_i，支持对两个序列单点修改，查询一个区间的 Ai+Ak−min⁡(Bj) (i<j<k)A_i+A_k-\min(B_j)\ (i<j<k) 最大值。

首先，由于外面的那层最大值，如果 BjB_j 不是最小那么一定不满足最大，所以式子可以简化成 Ai+Ak−BjA_i+A_k-B_j。

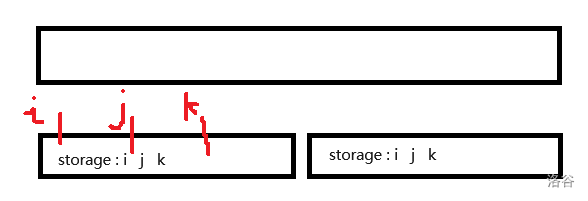
然后直接考虑如何合并区间标记。

第一种情况，合并后的 i,j,ki,j,k 在左右区间其中一个。

直接继承即可。

第二种情况，合并后的 i,j,ki,j,k 在不同区间。

其中 ii 或 kk 独占一个区间的情况本质相同，这里只分析 kk 独占一个区间的情况。

不难发现，此时 kk 可以是右区间任意数，最优情况是右区间最大值。这下只有 Ai−BjA_i-B_j 需要满足最大了，显然不能直接维护，仍然要拆标记。

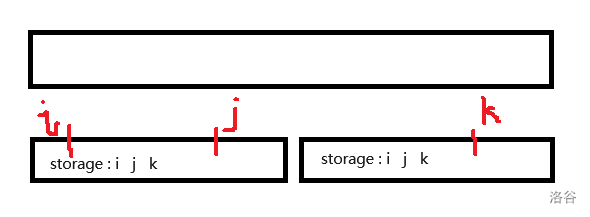
第一种情况和第一张图类似，直接继承即可。

第二种情况其实就是左区间的最大值减去右区间的最小值，相应维护就行了。

这样就解决这道题了。注意答案有可能为负数，初始值要设置正确。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
// Problem: P7706 「Wdsr-2.7」文文的摄影布置
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P7706
// Memory Limit: 256 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
const int maxn=5e5+5;
int a[maxn],b[maxn];
struct node{
	int ij,jk,maxA,minB,ans;
	void init(){ij=jk=ans=-1e9,maxA=-1e9,minB=1e9;}
}xds[maxn<<2];
node merge(node A,node B){
	node res;
	res.init();
	res.ij=max(A.maxA-B.minB,max(A.ij,B.ij));
	res.jk=max(B.maxA-A.minB,max(A.jk,B.jk));
	res.maxA=max(A.maxA,B.maxA);
	res.minB=min(A.minB,B.minB);
	res.ans=max(max(A.ij+B.maxA,A.maxA+B.jk),max(A.ans,B.ans));
	return res;
}
void pushup(int now){
	xds[now]=merge(xds[now<<1],xds[now<<1|1]);
	return;
}
void bulid(int now,int l,int r){
	xds[now].init();
	if(l==r)return xds[now].maxA=a[l],xds[now].minB=b[l],void();
	int mid=(l+r)/2;
	bulid(now<<1,l,mid);
	bulid(now<<1|1,mid+1,r);
	pushup(now);
	return;
}
void mdfA(int now,int l,int r,int q,int v){
	if(l==r)return xds[now].maxA=v,void();
	int mid=(l+r)/2;
	if(q<=mid)mdfA(now<<1,l,mid,q,v);
	else mdfA(now<<1|1,mid+1,r,q,v);
	pushup(now);
	return;
}
void mdfB(int now,int l,int r,int q,int v){
	if(l==r)return xds[now].minB=v,void();
	int mid=(l+r)/2;
	if(q<=mid)mdfB(now<<1,l,mid,q,v);
	else mdfB(now<<1|1,mid+1,r,q,v);
	pushup(now);
	return;
}
node q(int now,int l,int r,int sl,int sr){
	if(l==sl&&r==sr)return xds[now];
	int mid=(l+r)/2;
	node res;
	res.init();
	if(sl<=mid)res=merge(res,q(now<<1,l,mid,sl,min(mid,sr)));
	if(sr>mid)res=merge(res,q(now<<1|1,mid+1,r,max(sl,mid+1),sr));
	pushup(now);
	return res;
}
int main(){
	ios::sync_with_stdio(0);
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int i=1;i<=n;i++)cin>>b[i];
	bulid(1,1,n);
	int op,x,y;
	while(m--){
		// cerr<<m<<"\n";
		cin>>op>>x>>y;
		if(op==1)mdfA(1,1,n,x,y);
		else if(op==2)mdfB(1,1,n,x,y);
		else cout<<(q(1,1,n,x,y)).ans<<"\n";
	}
	return 0;
}

Trick 2: 复杂标记的处理

例题 1：P3215

首先想想询问怎么实现。

对于一个区间，如果我们知道其区间没有匹配的右括号前缀最大值和没有匹配的左括号的后缀最大值，那么答案就是 ⌈premax2⌉+⌈sufmax2⌉\lceil\frac{premax}{2}\rceil+\lceil\frac{sufmax}{2}\rceil。取左括号是 11，右括号为 −1-1，那么就是求区间前缀最小值和区间后缀最大值，那么合并的时候只需要对跨区间的区间操作进行处理就行了。注意到有翻转操作，那么需要维护前缀最大最小值和后缀最大最小值。

对于 Swap 操作，不难发现除翻转两个儿子外还需要前缀后缀的最值一一交换。

对于 Replace 操作，这个是简单的。

pushdown 时，还要考虑是先进行 swap 还是 replace。如果在打 replace 标记的时候清空 swap 标记，那么这个顺序其实没有什么影响。

最后就是最简单的 Invert 操作了，不难发现这种操作只有 22 种可能性，那么直接维护两种情况的信息就行了（开两颗平衡树就行了）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
// Problem: P3215 [HNOI2011] 括号修复 /  [JSOI2011]括号序列
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3215
// Memory Limit: 128 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+5;
int siz[maxn],sum[maxn],swa[maxn],premax[maxn],premin[maxn],sufmax[maxn],sufmin[maxn];
int rep[maxn],ch[maxn][2],val[maxn],pri[maxn];
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
int rt1,rt2,cnt;
int addP(int v){
	siz[++cnt]=1;
	sum[cnt]=v;
	val[cnt]=v;
	pri[cnt]=rnd();
	premax[cnt]=max(sum[cnt],premax[cnt]);
	premin[cnt]=min(sum[cnt],premin[cnt]);
	sufmax[cnt]=max(sum[cnt],sufmax[cnt]);
	sufmin[cnt]=min(sum[cnt],sufmin[cnt]);
	return cnt;
}
void pushup(int now){
	siz[now]=siz[ch[now][0]]+siz[ch[now][1]]+1;
	sum[now]=sum[ch[now][0]]+sum[ch[now][1]]+val[now];
	premax[now]=max(premax[ch[now][0]],sum[ch[now][0]]+val[now]+premax[ch[now][1]]);
	premin[now]=min(premin[ch[now][0]],sum[ch[now][0]]+val[now]+premin[ch[now][1]]);
	sufmin[now]=min(sufmin[ch[now][1]],sum[ch[now][1]]+val[now]+sufmin[ch[now][0]]);
	sufmax[now]=max(sufmax[ch[now][1]],sum[ch[now][1]]+val[now]+sufmax[ch[now][0]]);
	return;
}
void S(int x){
	swap(premax[x],sufmax[x]);
	swap(premin[x],sufmin[x]);
	return;
}
void sw(int x){
	swap(ch[x][0],ch[x][1]);
	S(x);
	swa[x]^=1;
	return;
}
void repl(int x,int v){
	sum[x]=siz[x]*v;
	val[x]=v;
	if(v==1)premax[x]=sufmax[x]=sum[x],premin[x]=sufmin[x]=0;
	else premin[x]=sufmin[x]=sum[x],premax[x]=sufmax[x]=0;
	rep[x]=v;
	swa[x]=0;
	return;
}
void pushdown(int x){
	if(rep[x]){
		if(ch[x][0])repl(ch[x][0],rep[x]);
		if(ch[x][1])repl(ch[x][1],rep[x]);
		rep[x]=0;
	}
	if(swa[x]){
		if(ch[x][0])sw(ch[x][0]);
		if(ch[x][1])sw(ch[x][1]);
		swa[x]=0;
	}
	return;
}
void split(int now,int k,int &x,int &y){
	if(!now)x=y=0;
	else{
		pushdown(now);
		if(siz[ch[now][0]]>=k)y=now,split(ch[now][0],k,x,ch[now][0]);
		else x=now,split(ch[now][1],k-siz[ch[now][0]]-1,ch[now][1],y);
		pushup(now);
	}
	return;
}
int merge(int x,int y){
	if(!x||!y)return x+y;
	else{
		if(pri[x]>pri[y]){
			pushdown(x);
			ch[x][1]=merge(ch[x][1],y);
			pushup(x);
			return x;
		}
		else{
			pushdown(y);
			ch[y][0]=merge(x,ch[y][0]);
			pushup(y);
			return y;
		}
	}
}
string s;
char o;
int getv(char u){
	if(u=='(')return 1;
	else return -1;
}
int n,m;
int main(){
	ios::sync_with_stdio(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>o;
		int vv=getv(o);
		rt1=merge(rt1,addP(vv));
		rt2=merge(rt2,addP(-vv));
	}
	int l,r,x,y,z,w;
	while(m--){
		cin>>s;
		if(s[0]=='R'){
			cin>>l>>r>>o;
			int vv=getv(o);
			split(rt1,r,x,y);
			split(x,l-1,z,w);
			repl(w,vv);
			rt1=merge(merge(z,w),y);
			split(rt2,r,x,y);
			split(x,l-1,z,w);
			repl(w,-vv);
			rt2=merge(merge(z,w),y);
		}
		else if(s[0]=='S'){
			cin>>l>>r;
			split(rt1,r,x,y);
			split(x,l-1,z,w);
			sw(w);
			rt1=merge(merge(z,w),y);
			split(rt2,r,x,y);
			split(x,l-1,z,w);
			sw(w);
			rt2=merge(merge(z,w),y);
		}
		else if(s[0]=='I'){
			cin>>l>>r;
			int xx,yy,zz,ww;
			split(rt1,r,x,y);
			split(x,l-1,z,w);
			split(rt2,r,xx,yy);
			split(xx,l-1,zz,ww);
			swap(w,ww);
			rt1=merge(merge(z,w),y);
			rt2=merge(merge(zz,ww),yy);
		}
		else{
			cin>>l>>r;
			split(rt1,r,x,y);
			split(x,l-1,z,w);
			cout<<ceil(abs(premin[w])/2.0)+ceil(abs(sufmax[w])/2.0)<<"\n";
			rt1=merge(merge(z,w),y);
		}
	}

	return 0;
}

代码可能有一些锅，数据真的很水。

例题 2：P7739

这个如如题要用矩阵，等我学了矩阵维护数列之后再来写。

回来啦！

这个题还是比较抽象的。

考虑对于一次转移，即 xy\frac{x}{y} 变为 yay+x\frac{y}{ay+x}，对于矩阵 [x   y][x\ \ \ y] 就是乘上 [a110]\begin{bmatrix} a & 1\\ 1 & 0 \end{bmatrix}。

那么不难发现初始值为 [1   0][1\ \ \ 0]，答案矩阵就是初始矩阵乘上操作矩阵在乘上 a=0a=0 和 11 的两个转移矩阵。

对于 W 操作，有 [1101]×[a110]=[a+1110]\begin{bmatrix} 1 & 1\\ 0 & 1 \end{bmatrix}\times\begin{bmatrix} a & 1\\ 1 & 0 \end{bmatrix}=\begin{bmatrix} a+1 & 1\\ 1 & 0 \end{bmatrix}。所以直接左乘一个 [1101]\begin{bmatrix} 1 & 1\\ 0 & 1 \end{bmatrix} 即可。考虑到这道题有翻转操作，所以在维护区间的时候要维护翻转后的乘积。那么直接按操作顺序正序与逆序都乘一遍就行了。（正序是放在右边乘，逆序是放在左边乘）

对于 E 操作，手玩一下可以发现两种情况最终变换出的结果是相同的。由于这种维护方式无法维护到倒数第二个数列的数到底是什么，所以直接对加数那种操作进行模拟。根据答案是逆序乘的原理，这个操作的答案矩阵也应该是该操作所有子操作的矩阵乘起来。加数和加减值前面都提到是什么矩阵，乘起来得到这个操作的矩阵是 [2−110]\begin{bmatrix} 2 & -1\\ 1 & 0 \end{bmatrix}。

对于翻转操作，除了翻转该节点自己的两个儿子，还要交换该节点自己的正序积和逆序积，并下传标记。

对于 FILP 操作，也是最简单的，直接维护两棵平衡树即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
// Problem: P7739 [NOI2021] 密码箱
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P7739
// Memory Limit: 1 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=6e5+5;
const int mod=998244353;
const int S=2;
struct matrix{
	int num[2][2];
	void clear(){
		for(int i=0;i<S;i++){
			for(int j=0;j<S;j++){
				num[i][j]=0;
			}
		}
		return;
	}
	void I(){
		for(int o=0;o<S;o++)num[o][o]=1;
		return;
	}
	matrix operator * (const matrix a) const{
		matrix res;
		res.clear();
		for(int i=0;i<S;i++){
			for(int j=0;j<S;j++){
				for(int k=0;k<S;k++){
					res.num[i][j]+=a.num[k][j]*num[i][k]%mod;
					res.num[i][j]+=mod;
					res.num[i][j]%=mod;
				}
			}
		}
		return res;
	}
	void out(){
		cout<<num[0][0]%mod<<" "<<num[0][1]%mod<<"\n";
		return;
	}
};
matrix rev[maxn],mul[maxn],mat[maxn];
bool tag[maxn];
int ch[maxn][2],pri[maxn],siz[maxn];
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
int rt1,rt2,cnt;
int addP(matrix v){
	mul[++cnt]=v;
	rev[cnt]=v;
	mat[cnt]=v;
	siz[cnt]=1;
	pri[cnt]=rnd();
	return cnt;
}
void pushup(int now){
	siz[now]=1+siz[ch[now][0]]+siz[ch[now][1]];
	mul[now]=mul[ch[now][0]]*mat[now]*mul[ch[now][1]];
	rev[now]=rev[ch[now][1]]*mat[now]*rev[ch[now][0]];
	return;
}
matrix W,E;
void pushrev(int now){
	swap(ch[now][0],ch[now][1]);
	swap(mul[now],rev[now]);
	tag[now]^=1;
	return;
}
void pushdown(int now){
	if(tag[now]){
		if(ch[now][0])pushrev(ch[now][0]);
		if(ch[now][1])pushrev(ch[now][1]);
		tag[now]=0;
	}
	return;
}
void split(int now,int k,int &x,int &y){
	if(!now)x=y=0;
	else{
		pushdown(now);
		if(siz[ch[now][0]]>=k)y=now,split(ch[now][0],k,x,ch[y][0]);
		else x=now,split(ch[now][1],k-siz[ch[now][0]]-1,ch[x][1],y);
		pushup(now);
	}
	return;
}
int merge(int x,int y){
	if(!x||!y)return x+y;
	else{
		if(pri[x]>pri[y]){
			pushdown(x);
			ch[x][1]=merge(ch[x][1],y);
			pushup(x);
			return x;
		}
		else{
			pushdown(y);
			ch[y][0]=merge(x,ch[y][0]);
			pushup(y);
			return y;
		}
	}
}
char c;
string s;
int l,r;
matrix ned1,ned2,ans;
signed main(){
	ios::sync_with_stdio(0);
	for(int i=0;i<maxn;i++)rev[i].I(),mul[i].I(),mat[i].I();
	W.clear();
	W.I(),W.num[0][1]=1;
	E.clear();
	E.num[0][0]=2,E.num[0][1]=-1,E.num[1][0]=1;
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>c;
		if(c=='W'){
			rt1=merge(rt1,addP(W));
			rt2=merge(rt2,addP(E));
		}
		else{
			rt1=merge(rt1,addP(E));
			rt2=merge(rt2,addP(W));
		}
	}
	ned1.num[0][0]=1;
	ned2=W;
	ans=ned1*rev[rt1]*ned2;
	ans.out();
	int x,y,z,w,xx,yy,zz,ww;
	while(m--){
		cin>>s;
		if(s[0]=='A'){
			cin>>c;
			if(c=='W'){
				rt1=merge(rt1,addP(W));
				rt2=merge(rt2,addP(E));
			}
			else{
				rt1=merge(rt1,addP(E));
				rt2=merge(rt2,addP(W));
			}
		}
		else if(s[0]=='F'){
			cin>>l>>r;
			split(rt1,r,x,y);
			split(x,l-1,z,w);
			split(rt2,r,xx,yy);
			split(xx,l-1,zz,ww);
			swap(ww,w);
			rt1=merge(merge(z,w),y);
			rt2=merge(merge(zz,ww),yy);
		}
		else{
			cin>>l>>r;
			split(rt1,r,x,y);
			split(x,l-1,z,w);
			pushrev(w);
			rt1=merge(merge(z,w),y);
			split(rt2,r,x,y);
			split(x,l-1,z,w);
			pushrev(w);
			rt2=merge(merge(z,w),y);
		}
		ans=ned1*rev[rt1]*ned2;
		ans.out();
	}
	return 0;
}

Trick 3: 矩阵维护数列

这个是我自己加的。

通常来讲，一道题的修改都是线性变换时可以使用矩阵来维护数列。

最通俗的理解，就是一个矩阵每一列是对应参数的系数，每一行是变换后最终的数。

比如说区间加，区间赋值，区间赋值为另一个数列的 kk 倍，区间乘都可以维护：

（按顺序）

[1v01]\begin{bmatrix} 1 & v\\ 0 & 1 \end{bmatrix}

（横 1 是区间和，横 2 是区间长度）

[0v01]\begin{bmatrix} 0 & v\\ 0 & 1 \end{bmatrix}

（横 1 是区间和，横 2 是区间长度）

[0k0010001]\begin{bmatrix} 0 & k & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}

（横 1 是区间和，横 2 是赋值数列区间和，横 3 是区间长度）

[k001]\begin{bmatrix} k & 0\\ 0 & 1 \end{bmatrix}

（横 1 是区间和，横 2 是区间长度）

当然还有一些复杂一点的。

典题：P7453 大魔法师

对于每一个操作的矩阵：

（横 1 是 AA 区间和，横 2 是 BB 区间和，横 3 是 CC 区间和，横 4 为区间长度）

[1100010000100001]\begin{bmatrix} 1 & 1 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}

[1000011000100001]\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 1 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}

[1000010010100001]\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 1 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}

[100v010000100001]\begin{bmatrix} 1 & 0 & 0 & v\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}

[10000v0000100001]\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & v & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}

[10000100000v0001]\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & v\\ 0 & 0 & 0 & 1 \end{bmatrix}

注意到代码中用的答案矩阵是横着的，为了更好地维护信息，最好选择这样，能规避左乘带来的奇怪问题，尽量转化成右乘，所以矩阵都要沿对角线对称一下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
// Problem: P7453 [THUSCH2017] 大魔法师
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P7453
// Memory Limit: 500 MB
// Time Limit: 5000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int mod=998244353;
const int S=4;
struct an{
	int a,b,c;
	void init(){
		a=0,b=0,c=0;
		return;
	}
	an operator + (const an p)const{
		an res;
		res.init();
		res.a=p.a+a;
		res.b=p.b+b;
		res.c=p.c+c;
		return res;
	}
};
struct matrix{
	int num[S][S];
	void clear(){
		for(int i=0;i<S;i++)for(int j=0;j<S;j++)num[i][j]=0;
		return;
	}
	void I(){
		clear();
		for(int i=0;i<S;i++)num[i][i]=1;
		return;
	}
	bool operator == (const matrix a) const {
		for(int i=0;i<S;i++){
			for(int j=0;j<S;j++){
				if(a.num[i][j]!=num[i][j])return 0;
			}
		}
		return 1; 
	}
	matrix operator * (const matrix a) const {
		matrix res;
		res.clear();
		for(int i=0;i<S;i++){
			for(int j=0;j<S;j++){
				for(int k=0;k<S;k++){
					res.num[i][j]+=a.num[k][j]*num[i][k];
				}
				res.num[i][j]%=mod;
			}
		}
		return res;
	}
	matrix operator + (const matrix a) const {
		matrix res;
		res.clear();
		for(int i=0;i<1;i++){
			for(int j=0;j<S;j++){//maxi=0
				res.num[i][j]=num[i][j]+a.num[i][j];
				res.num[i][j]%=mod;
			}
		}
		return res;
	}
	void P(){
		for(int i=0;i<S;i++){
			for(int j=0;j<S;j++){
				cout<<num[i][j]<<" ";
			}
			cout<<"\n";
		}
		return;
	}
	void _4(int v){
		num[3][0]=v;
		return;
	}
	void _5(int v){
		num[1][1]=v;
		return;
	}
	void _6(int v){
		num[3][2]=v;
		return;
	}
	void init(int a,int b,int c){
		num[0][0]=a;
		num[0][1]=b;
		num[0][2]=c;
		num[0][3]=1;
		return;
	}
	an getans(){
		return {num[0][0],num[0][1],num[0][2]};
	}
};
const int maxn=2.5e5+5;
matrix I,_1,_2,_3,_4,_5,_6,org[maxn];
matrix xds[maxn<<2],lazy[maxn<<2];
void prework(){
	I.I();
	_1.I();
	_2.I();
	_3.I();
	_4.I();
	_5.I();
	_6.I();
	_1.num[1][0]=1;
	_2.num[2][1]=1;
	_3.num[0][2]=1;
	_6.num[2][2]=0;
	return;
}
int n,m;
void pushup(int now){
	xds[now]=xds[now<<1]+xds[now<<1|1];
	return;
}
void pushdown(int now,int l,int r){
//	if(lazy[now]==I){
		xds[now<<1]=xds[now<<1]*lazy[now];
		xds[now<<1|1]=xds[now<<1|1]*lazy[now];
		lazy[now<<1]=lazy[now<<1]*lazy[now];
		lazy[now<<1|1]=lazy[now<<1|1]*lazy[now];
		lazy[now].I();
	//}
	return;
}
void bulid(int now,int l,int r){
	lazy[now].I();
	if(l==r)return xds[now]=org[l],void();
	int mid=(l+r)/2;
	bulid(now<<1,l,mid);
	bulid(now<<1|1,mid+1,r);
	pushup(now);
	return;
}
void mdf(int now,int l,int r,int sl,int sr,matrix v){
	//cerr<<l<<" "<<r<<"\n";
	if(l==sl&&r==sr){
		xds[now]=xds[now]*v;
		lazy[now]=lazy[now]*v;
		return;
	}
	pushdown(now,l,r);
	int mid=(l+r)/2;
	if(sl<=mid)mdf(now<<1,l,mid,sl,min(sr,mid),v);
	if(sr>mid)mdf(now<<1|1,mid+1,r,max(mid+1,sl),sr,v);
	pushup(now);
	return;
}
an q(int now,int l,int r,int sl,int sr){
	if(l==sl&&r==sr)return xds[now].getans();
	pushdown(now,l,r);
	int mid=(l+r)/2;
	an res;
	res.init();
	if(sl<=mid)res=res+q(now<<1,l,mid,sl,min(mid,sr));
	if(sr>mid)res=res+q(now<<1|1,mid+1,r,max(mid+1,sl),sr);
	pushup(now);
	return res;
}

signed main(){
	ios::sync_with_stdio(0);
	prework();
	cin>>n;
	int a,b,c,op;
	for(int i=1;i<=n;i++){
		cin>>a>>b>>c;
		org[i].init(a,b,c);
	}
	bulid(1,1,n);
	cin>>m;
	
	while(m--){
		// xds[1].P();
		//cerr<<m<<"\n";
		cin>>op>>a>>b;
		if(op==1){
			mdf(1,1,n,a,b,_1);
		}else if(op==2){
			mdf(1,1,n,a,b,_2);
		}else if(op==3){
			mdf(1,1,n,a,b,_3);
		}else if(op==4){
			cin>>c;
			_4._4(c);
			mdf(1,1,n,a,b,_4);
		}else if(op==5){
			cin>>c;
			_5._5(c);
			mdf(1,1,n,a,b,_5);
		}else if(op==6){
			cin>>c;
			_6._6(c);
			mdf(1,1,n,a,b,_6);
		}else{
			an buf=q(1,1,n,a,b);
			cout<<buf.a%mod<<" "<<buf.b%mod<<" "<<buf.c%mod<<"\n";
		}
	}
	return 0;
}

Trick 4: pre数组的技巧

这种思想差不多就是对于一个询问，按右端点排序之后，我们完全可以只关注出现过的数的最右边的那个就行了。

也就是说读取到一个数时，如果前面已经出现过这个数，直接把这个数产生的贡献删除，再加入当前点的贡献，本质是一种时间线上的离线扫描线。

预处理时要预处理出这个数之前在哪里出现过，即 pre 数组，通常用于去除重复贡献。

板子题：P1972 HH 的项链

一句话：贡献的加入和删除直接在下标上完成（即指当前该位置上是否可能对答案有贡献），询问时直接区间和就行了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
// Problem: P1972 [SDOI2009] HH的项链
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1972
// Memory Limit: 512 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int n;
int t[1000001];
int lowbit(int x){
	return x&-x;
}
void mdf(int x,int v){
	if(x==0)return;
	while(x<=n){
		t[x]+=v;
		x+=lowbit(x);
	}
	return;
}
int q(int x){
	int res=0;
	while(x>0){
		res+=t[x];
		x-=lowbit(x);
	}
	return res;
}
int pre[1000001];
int a[1000001],nxt[1000001];
int ans[1000001];
vector<pair<int,int> > L[1000001];
int m,l,r;
int main(){
	ios::sync_with_stdio(0);
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		if(nxt[a[i]])pre[i]=nxt[a[i]];
		nxt[a[i]]=i;
	}
	cin>>m;
	for(int i=1;i<=m;i++){
		cin>>l>>r;
		L[r].push_back(make_pair(l,i));
	}
	for(int i=1;i<=n;i++){
		mdf(pre[i],-1);
		mdf(i,1);
		int std=q(i);
		for(auto p:L[i]){
			ans[p.second]=std-q(p.first-1);
		}
	}
	for(int i=1;i<=m;i++)cout<<ans[i]<<"\n";
	return 0;
}

lxl 的例题：P6617

考虑开始的时候记录最近的一个数与该数和为 ww。然后发现没法修改，这个时候不难发现如果最近的和为 ww 的数比最近的相同的数远，可以将这个数的 prepre 设置为 00，这样就能保证修改复杂度正确。

对于修改，使用 set 作为桶维护数再哪些地方出现，然后大力分讨即可。可能出现改变的 prepre 只有五个：本身，原数的后面的第一个相等和和为 ww 的数，新数的后面的第一个相等和和为 ww 的数。

细节较多，注意合理使用哨兵。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
// Problem: P6617 鏌ユ壘 Search
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P6617
// Memory Limit: 128 MB
// Time Limit: 1000 ms
// Start coding at 2023-11-30 20:40:25
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
int pre[500005],nxt[500005],a[500005];
set<int> s[500005];
int xds[2000200];
int n,m,w;
void pushup(int now){
	xds[now]=max(xds[now<<1],xds[now<<1|1]);
	return;
}
void bulid(int now,int l,int r){
	if(l==r)return xds[now]=pre[l],void();
	int mid=(l+r)/2;
	bulid(now<<1,l,mid);
	bulid(now<<1|1,mid+1,r);
	pushup(now);
	return;
}
void mdf(int now,int l,int r,int q,int v){
	if(q>n||q<1)return;
	if(l==r)return xds[now]=v,void();
	int mid=(l+r)/2;
	if(q<=mid)mdf(now<<1,l,mid,q,v);
	else mdf(now<<1|1,mid+1,r,q,v);
	pushup(now);
	return;
}
int qmax(int now,int l,int r,int sl,int sr){
	if(l==sl&&r==sr)return xds[now];
	int mid=(l+r)/2,res=0;
	if(sl<=mid)res=max(res,qmax(now<<1,l,mid,sl,min(sr,mid)));
	if(sr>mid)res=max(res,qmax(now<<1|1,mid+1,r,max(sl,mid+1),sr));
	pushup(now);
	return res;
}
int op,x,y,C;
set<int>::iterator it,ot;
int main(){
	ios::sync_with_stdio(0);
	cin>>n>>m>>w;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		s[a[i]].insert(i);
		if(nxt[a[i]]<=nxt[w-a[i]])pre[i]=nxt[w-a[i]];
		nxt[a[i]]=i;
	}
	bulid(1,1,n); 
	for(int i=0;i<=w;i++)s[i].insert(0),s[i].insert(n+1);
	while(m--){
		cin>>op>>x>>y;
		if(op==1){
			if(a[x]==y)continue;
//			if(y==w/2)return 0;
			// int org=a[x];
			s[a[x]].erase(x);
			/*Deal with itself*/
			it=s[w-y].upper_bound(x);
			it--;
			ot=s[y].upper_bound(x);
			ot--;
			if(*it>=*ot)mdf(1,1,n,x,*it);
			else mdf(1,1,n,x,0);
//			cout<<*it<<"\n";
			/*Deal with orginal pre*/
			it=s[a[x]].lower_bound(x);
			ot=s[w-a[x]].lower_bound(x);
			if(*it>=*ot){
				it--,ot--;
				if(*it>=*ot)mdf(1,1,n,*(++ot),*it);
				else mdf(1,1,n,*(++ot),0);
			}
			else{
				it--,ot--;
				if(*it>=*ot)mdf(1,1,n,*(++it),0);
				else mdf(1,1,n,*(++it),*ot);
			}
			/*Deal with new pre*/
			a[x]=y;
			s[a[x]].insert(x);
			it=s[a[x]].upper_bound(x);
			ot=s[w-a[x]].upper_bound(x);
			if(*it>=*ot)mdf(1,1,n,*ot,x);
			else mdf(1,1,n,*it,0);
		}else{
			x^=C,y^=C;
//			if(y<x)return 0;
//			cout<<x<<" "<<y<<" "<<qmax(1,0,n,x,y)<<" "<<"\n";
			if(qmax(1,1,n,x,y)>=x){
				cout<<"Yes\n";
				C++;
			}
			else cout<<"No\n";
		}
	}
	return 0;
}

均摊